Category: Totally Useless Charts

Categories
Design How Did You Build That in Tableau? How-To's Tableau Techniques Totally Useless Charts Uncategorized

3 Ways to Build Gradients in Tableau

3 Ways to Build Gradients in Tableau by Brian Moore

A few years back I came across this beautiful, impactful viz by the incredibly talented Ivett Kovács. I was already amazed by the design, but when I realized that those gradient circles weren’t custom shapes, but actually built directly in Tableau using standard mark types, my mind was blown. I was brand new to the Tableau Community when this viz was published, and it was one of the first truly custom visualizations I had ever seen built entirely in Tableau. It was one of those AHA moments that you look back on years later and realize just how much of an impact it had on you. It was a sudden realization that with a little math and a little creativity, you can create things in Tableau that really just don’t seem possible…until somebody does it.

Screenshot of Ivett Kovacs "Sorry Sweetie" visualization

In her visualization (and her blog post about gradients), Ivett credits another amazingly talented individual, Ludovic Tavernier, for this gradient color concept. Ken & Kevin Flerlage have also done a lot of really cool stuff in Tableau with gradients. So I, in no way, shape, or form, invented the concept of creating gradients in Tableau. But, over the past couple of years, I have taken that concept and come up with a few different techniques for applying it in Tableau.

In this blog post, I’m going to cover 3 different methods. We’ll call them the No-Math Method, the Straight-Line Method, and the Vertex Method. If you would like to follow along with this post and build these yourself, you can download the sample data here and download the sample workbook here.

But before we get started, a quick disclaimer. Like most of the things I share on Tableau Public, I would never, ever, ever try to do something like this at work. Adding gradients to your charts will not make them better at communicating important information. They will, however, make them load much, much slower. All of the techniques we’re going to discuss today rely on data densification, where we are going to blow up our data source and create a bunch of new records that we can use to draw the lines and shapes needed to create that gradient effect. Also, if you don’t have any experience with data densification, or drawing curved lines and/or polygons, I would recommend checking out part 1 of the 3-part blog series below. Not required, but it might help.

Fun With Curves in Tableau Part 1: Circles
Fun With Curves in Tableau Part 2: Bezier Curves
Fun With Curves in Tableau Part 3: Sigmoid Curves

Creating Your Color Palettes

This part is totally optional. The foundation of any of these methods, or the methods created by others before me, is that we are basically placing a bunch of overlapping but slightly offset marks on the Tableau canvas, and then assigning a sequential color palette to create that gradient effect. The measure we use on color will go from a lower value to a higher value, and that value will align with the shade the color (so low values have a lighter shade and high values have a darker shade or vice versa). So, in order for this to work, we need to have a sequential color palette available for each color we want to use in our viz. Tableau already has many of these available so you don’t necessarily need to create your own, but if you have custom colors that you want to use, this is how I would go about setting up your palettes.

The nice thing about sequential color palettes is that we really only need two color codes to build our gradients. We need a light shade on one end and a dark shade on the other end, and Tableau will automatically fill in all of the shades in between. One option to get these codes is to use an online color shade generator, like this one. You can enter your “base” color and then select a lighter shade and a darker shade to use in your palette. But I like to play around with the shades and see exactly how it’s going to look when I bring it in to Tableau. This way I can kind of lock it in before editing my preferences file and cut down on the back and forth that goes with editing color palettes. This is how I build and test my sequential palettes using PowerPoint

Building a Sequential Color Palette in PowerPoint

  • Open PowerPoint
  • Click on Insert > Shapes and select the Circle shape type
  • Format the Circle
    • Increase the size so you can see the gradient better (I set it to around 4 x 4 inches)
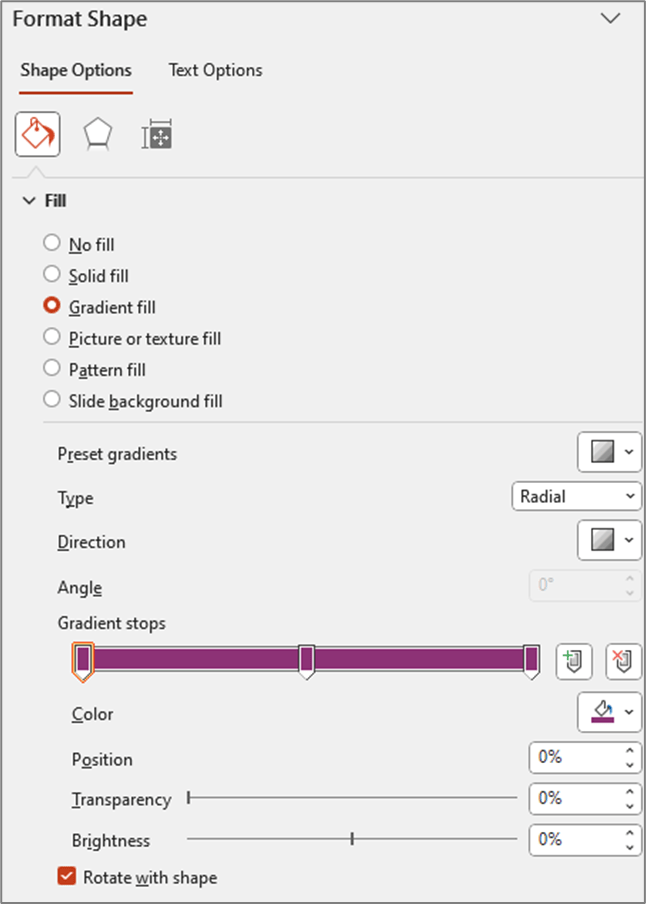
    • Right click on shape and select “Format Shape”
    • Change the “Fill” type to “Gradient Fill”
    • Change the “Type” to “Radial”
    • For “Direction” choose the center option (gradient radiates from the center of the shape)
    • Change the number of “Gradient stops” to 3 (add or delete stops so that you have a total of 3)
    • Click on each of the stops and set the color to your “base” color (in my example the base color is #8D3276)
    • Update Position of Each Stop
      • Stop 1: 0%
      • Stop 2: 50%
      • Stop 3: 100%

At this point your settings should look something like this and your shape should be a circle that appears to be one solid color (even though it is set to Gradient)

Screenshot displaying the correct formatting options for Step 1 of creating a color palette in PowerPoint
  • Edit the stop colors
    • Edit stop #1
      • Click on the 1st stop to select it
      • Below the stops click on the Color selector
      • Click on “More Colors”
      • Click on the “Custom” tab
      • Click and drag the arrow next to the color bar upward to change to a lighter shade of your “base” color
    • Edit stop #3
      • Click on the last stop to select it
      • Below the stops click on the Color selector
      • Click on “More Colors”
      • Click on the “Custom” tab
      • Click and drag the arrow next to the color bar downward to change to a darker shade of your base color

This is how my color selectors look for the 1st and last (3rd) stops

Screenshots showing color selections for first and last stop in gradient

And here is what my gradient circle looks like

Image showing the applied gradient effect and the three selected color shades

You can continue clicking on the 1st and 3rd stops and tweaking the shades lighter and darker until you have a gradient you are happy with. And then we just need to add these colors to our preferences file as a sequential color palette. You don’t have to include the “base” color, but I like to include it so I have it if I need to edit my palette later on.

  • Go to Documents > My Tableau Repository
  • Right click on your Preferences file and open with a Text Editor program (like Notepad)
  • Add the palette to the end of your preferences file before the line containing the </preferences> closing tag
  • The palette should be in the format below
Screenshot displaying the correct format for adding color palettes to Tableau preferences file

Once your palette is added, close out of Tableau and re-open it. I have put a sample preferences file with a few of these gradient palettes in a Google Drive folder here.

Choosing the right Method

As I mentioned earlier, this post is going to cover three different methods for building gradients in Tableau. Which one is best? Well, as with most things Tableau…it depends.

The No-Math Method

I really like the No-Math method. It’s by far the easiest to implement, requires no complicated calculations, and it can be used on different mark types (gradient lines, bars, etc.). The only real downside is that you can’t really control the direction of the gradient or the “position” of the light source. With this method, the gradient will always be lightest in the center and darkest on the edges, as if the light source was shining from directly in front of the object. Another nice thing about this method is that you don’t have to worry about the size/shape of your view. In the other methods we are “drawing” the circles, so the X and Y axis ranges need to be equal, and the Height and Width of the view need to be equal when placed on the dashboard. Otherwise, you will end up with ovals instead of circles. But with this method we are using the Circle mark type, so we don’t have to worry about any of that.

An example of the No-Math method gradient
The Straight-Line Method

This method requires a little bit of math, but nothing too complicated. It’s definitely easier than the Vertex Method, but more difficult than the No-Math method. This method provides some flexibility on the gradient direction, but the main limitation is that the gradient has to start on one edge of the object. With this method, the gradient will always be lighest on one edge and darkest on the opposite edge, as if the light source was shining from the side of the object.

An example of the Straight-Line method gradient
The Vertex Method

This method is by far the most complicated, but it’s also my favorite, as it gives you the most flexibility in terms of design. With this method you can use parameters to “move” the light source so that it looks like the light is shining on the object from any direction, giving it a much more realistic 3D look compared to any of the other methods. But, just for reference, the no-math method uses 3 calculations, the straight-line method uses 7 calculations, and this method uses almost 20.

An example of the Vertex method gradient

Method 1: The No-Math Method

Of the three methods in this post, this is the only one that does not use the Line mark type. The way that this one works is that we are basically stacking a bunch of circles right on top of each other. Each circle is a slightly different size and a slightly different shade of our “base” color. The smallest, and lightest colored circle will be on the top of the stack, and the largest, darkest colored circle will be on the top of the stack.

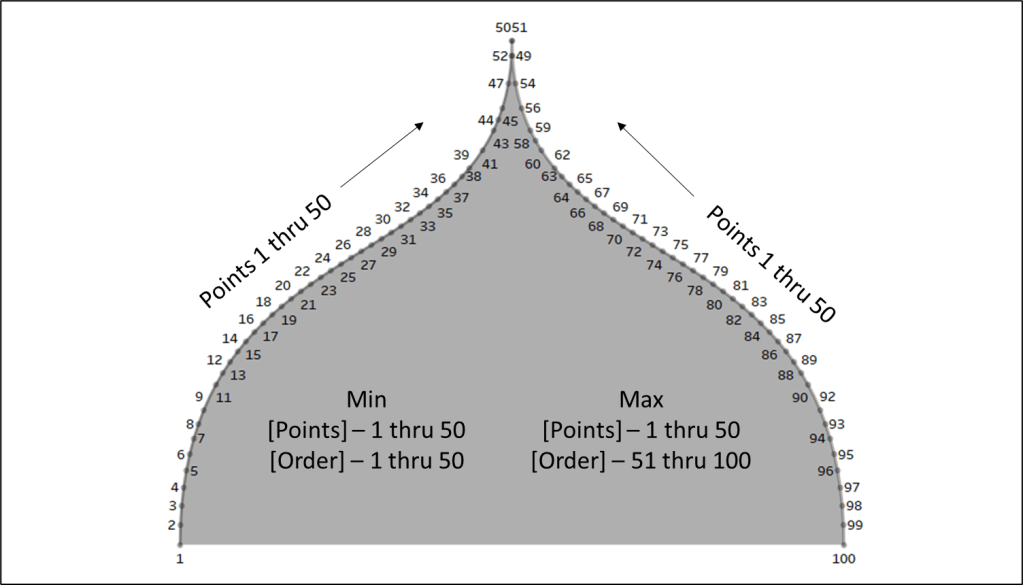
If you haven’t already I would recommend downloading the base data and sample workbook. Our base data (Method 1 Data) is a simple file with just 9 records. We have a Dimension field and a Size field (and a few other fields that aren’t required). And then we have a Densification table (Method 1 Densification), with 100 records and one column called “Points”. To build our Data source we are going to do a Physical join between these two tables by creating a join calculation, with a value = 1, on each side of the join. The result will be a data source with 900 records (100 densification records for each of our 9 data source records). It should look like this.

Screenshot displaying the correct joins for Method 1

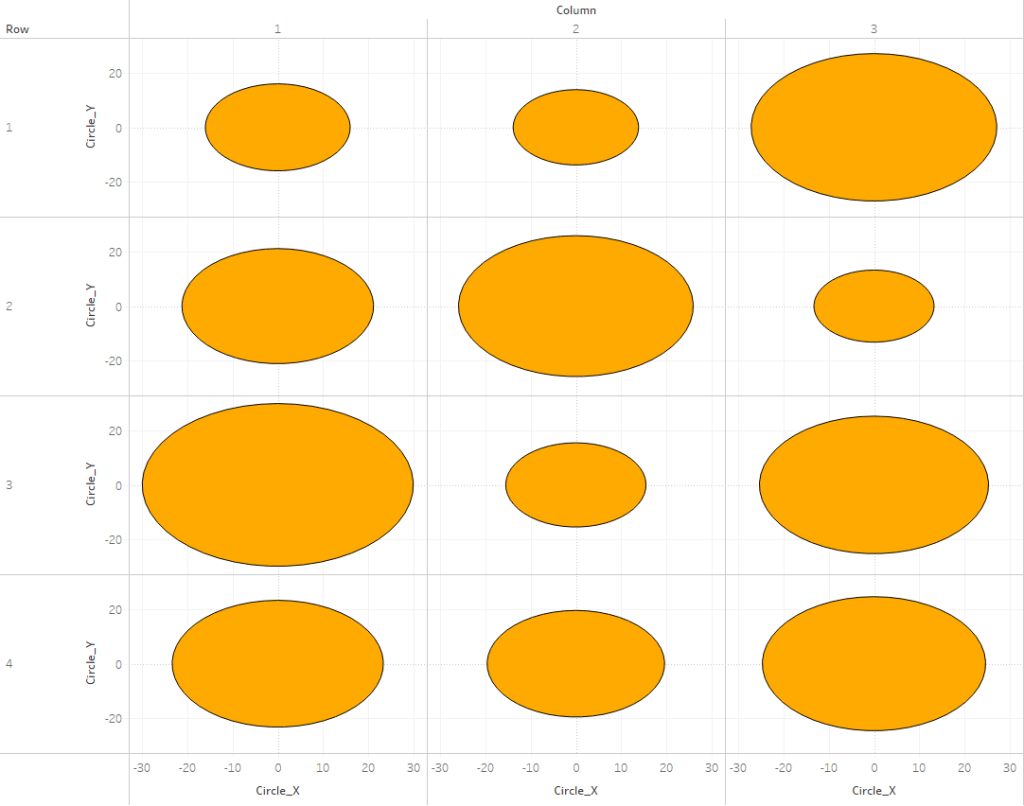
Now this part may get a little confusing as we’re going to be talking about two different types of circles here. So, for the rest of these section, I am going to refer to the main gradient circles that we are trying to create as “Design Circles” and the individual circles used to create the gradient effect as “Building Circles”. So in all of the screenshots above, those 9 gradient circles are our “Design Circles”, and each of those is made up of 100 “Building Circles”.

The exact way that you build this is going to depend on how your chart is set up. In this example, we are going to build a simple 3 x 3 Panel chart, using the Size field to determine the size of our “Design Circles”. So to build my panel, I’m going to use some of those extra columns from my data source (row and column, but these could be easily calculated in the workbook instead). I’ll change them both to dimensions and bring them out on to the Rows and Columns shelves respectively.

Also, on each of these shelves, I’m going to double click in the blank space on the shelf and enter MIN(0.0). The reason for this is that we need to have a numeric measure on columns and/or rows to be able to “stack” these marks on top of each other. Otherwise we’ll end up with a unit chart with 100 circles next to each other. However, if you were building a scatterplot, or something like that where you already have numeric measures on rows and/or columns, you would not need to do this. So to start, my rows and column shelves are going to look like this.

Screenshot displaying the correct pills for the Column and Rows shelves

Next, let’s build the calculations we’re going to need for the size and color of each of our circles. First, we’re going to build an L.O.D. to get the maximum number of densification records (in our case, this will be 100)

Max Points = {MAX([Points])}

Now we’ll build a calculated field that determines the size of every “Building Circle”. So we already determined that we are going to use the [Size] field to determine the size of our “Design Circles”. So we need our largest “Building Circle” to have that same value. And then we want the size of the rest of our “Building Circles” to get smaller and smaller. In our densification table, we have 100 records with values from 1 to 100. So if we divide each of those values by the maximum value (in our case that’s 100) that will give us percentages from 1% to 100%. And then if we multiply that by our [Size] field, we’ll end up with 100 different values, with the largest value being equal to the [Size] field, and the smallest value being equal to 1% of that value. But note that you do not need exactly 100 records for this to work. Your densification table could have 200 records. The largest circle will still have the same value as the [Size] field, and the smallest would be equal to .5% of that value. Or it could have 1000 records. Or it could have 53,469 records. It doesn’t matter, as long as the numbers in the [Points] field are sequential and you’re dividing each [Points] value by the maximum [Points] value.

Circle Size = ([Points]/[Max Points])*[Size]

And then lastly we need a field to use on Color. The logic here is basically the same as our [Circle Size] calculation. We’re just dividing the [Points] value by the maximum value to get 100 evenly spaced values from 1% to 100%

Color = [Points]/[Max Points]

Now, let’s build our view

  • If you haven’t already, complete the first few steps mentioned above (drag rows/columns to shelves, add MIN(0.0) to both shelves)
  • Right click on [Points] and “Convert to Dimension”
  • Drag [Points] to Detail on the Marks Card
  • Set Mark Type to “Circle” on the Marks Card
  • Drag [Circle Size] to Size on the Marks Card
  • Drag [Color] to Color on the Marks Card
  • Edit the Colors
    • Click on the Color card and select Edit Colors
    • Select your sequential color palette from the “Palette” drop-down
    • Click on Advanced and tweak the “End” value
      • Using the standard color range usually results in the outer edge being too dark
      • If you want the gradient to match the one in PowerPoint, set the “End” value to somewhere between 1.5 and 2

When complete, your worksheet should look something like this

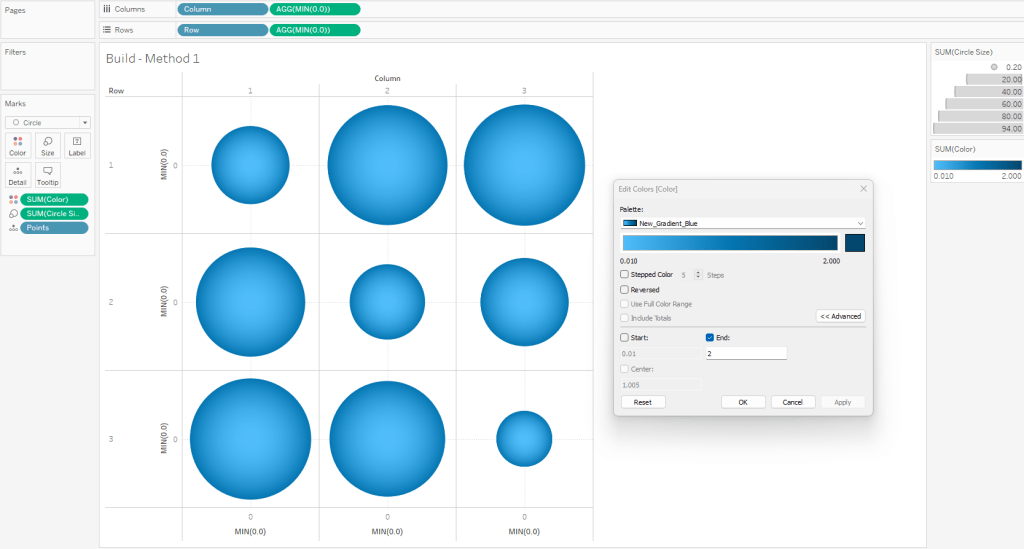
Screenshot of Method 1 worksheet

To illustrate how this method works, this is what this view would look like if we put the [Points] field on Color as a Dimension. You can see that each of our “Design Circles” is made up of 100 different “Building Circles”, each slightly bigger than the one on top of it and slightly smaller than the one below it.

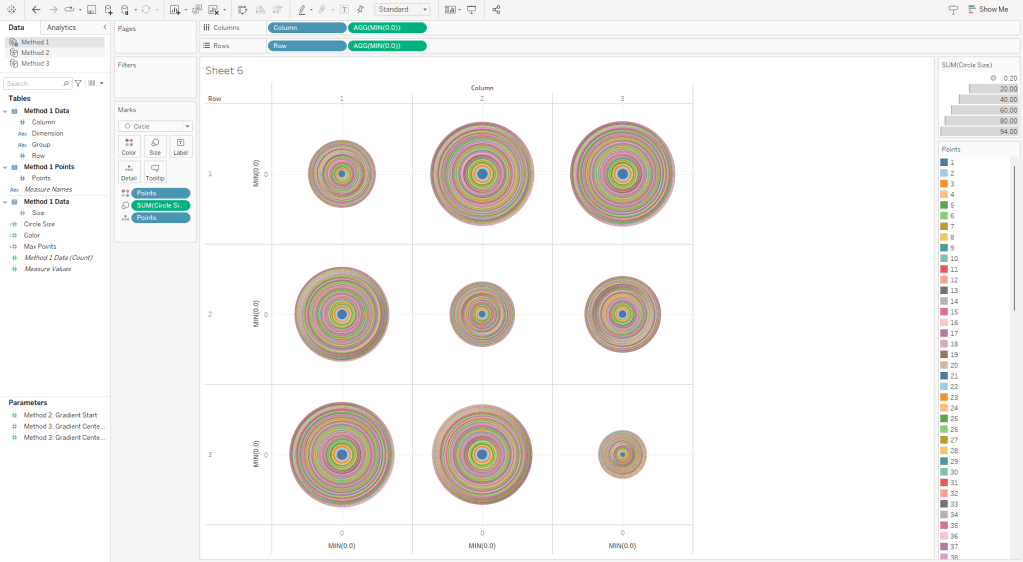
Alternative screenshot for Method 1 if a different color was applied to each circle

Method 2: The Straight-Line Method

On to Method #2. As I mentioned earlier, this method is going to use lines to create the gradient effect. In Method #1, we stacked 100 circles on top of each other. In Method #2, we are going to place 600 lines right next to each other.

The data source set up for this method is very similar to Method #1, except that it has 600 densification records instead of 100, and we are going to add an additional “table”. This “table” just has 1 field called [Order] and just two records (with values of 1 and 2). Alternatively you could just add this column to the Densification table and have two records for each [Points] value, but it’s a lot easier to increase or decrease the number of densification records (which I do pretty frequently) if you put this in it’s own table. So again, we are going to do a Physical join between our data table and our densification table and then we’ll add another join for our order table (once again using the join calculation).

Screenshot displaying the correct joins for Method 2

As I mentioned earlier, the main limitation of this method is that the gradient has to start on one edge of the circle. But I like to make it dynamic so you can tweak where that starting edge is (top/bottom/left/right/etc.). So I use a numeric parameter where the range of acceptable values is between 0 and 1. This will be used to rotate the circle between 0% and 100%.

Screenshot of the parameter used to rotate the gradient in Method 2

Now we’ll start building our calculations. The first one is going to be our [Max Points] field, which is the same as the one in Method #1

Max Points = {MAX([Points])}

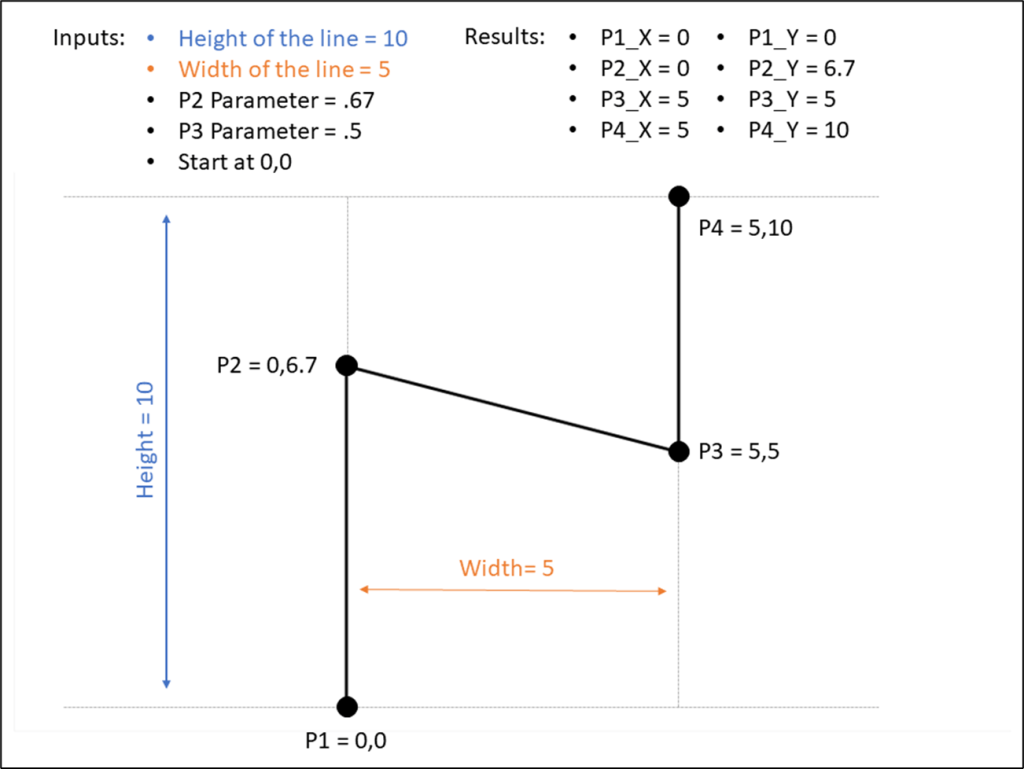
In order to draw a circle in Tableau (check out the blog post at the beginning of this article if you haven’t already) using the method that I typically use, we need two inputs: radius and position. Let’s start with the radius. Once again we are going to use the [Size] field to size our circles, and that value is going to represent the Area of the circle. So if the [Size] field is the Area, then we can calculate the radius using the calculation below

Radius = SQRT([Size]/PI())

Now, the position. The position is a value between 0 and 1 (or 0% to 100%) that represents how far around the circle that point would appear. So 25% would be at 90 degrees, or 3 o’clock, 50% would be at 180 degrees, or 6 o’clock, and so on. So to get that value, similar to how we calculated the color and size in Method 1, we can just divide the [Points] value by the maximum [Points] value (and subtract 1 from both the numerator and denominator to start at exactly 0%). Let’s call this [Position_Base]

Position_Base = (([Points]-1)/([Max Points]-1))

Now if we were to plug our [Radius] and [Position_Base] fields into our X and Y calcs (which I will get to in a minute), we would end up with something like this. To make it a little easier to see, for this example, I limited the number of densification records to 50. So we end up with 50 points evenly spaced around a circle.

Screenshot showing how the points are plotted to create the circular shape

But now we need to adjust those positions a bit. Ultimately, what we want to do is to draw perpendicular lines across the circle. So in the example image above, we would want to draw a line from 1 to 50 (50 is hidden behind 1 in the image), another line from 2 to 49, then 3 to 48, and so on until we get all the way around the circle. So let’s start by getting all of our points on 1 side of the circle. And we’ll do that by dividing our [Position_Base] field in half. And we’ll call it [Position_Offset]

Position_Offset = [Position_Base]/2

So now, instead of our points being evenly spread between 0% and 100% around the circle, they are spread between 0% and 50%, with all of the points on the same side of the circle.

Screenshot showing all of the points moved to the right hand side after we divide Position Base in half

And now here is where our [Order] field comes in from that new table we added. Each of the points in the screenshots above actually consists of 2 records, one where [Order]=1 and one where [Order]=2. So we are going to create one more calculation that will basically create a mirror image of these points so that each [Point] value from our densification table has one mark on the right side of the circle, and then a second mark on the mirror opposite side of the circle. And this will be our final [Position] calc.

Position = if [Order]=1 then [Position_Offset] else 1-[Position_Offset] END + [Method 2: Gradient Start]

So if [Order]=1 we’ll use that position on the right side of the circle that we calculated previously. If [Order]=2, we’ll subtract that value from 1 to give us the position that is the mirror opposite of it on the circle. So for example, if our [Order]=1 mark is at 10%, the [Order]=2 mark would be at 90%. If 1 is at 35%, then 2 is at 65% and so on. And then finally, we add the value from the parameter we created earlier (in the screenshot below it is set to 0%) to “rotate” the circle. And then if we connected those marks, it would look something like this.

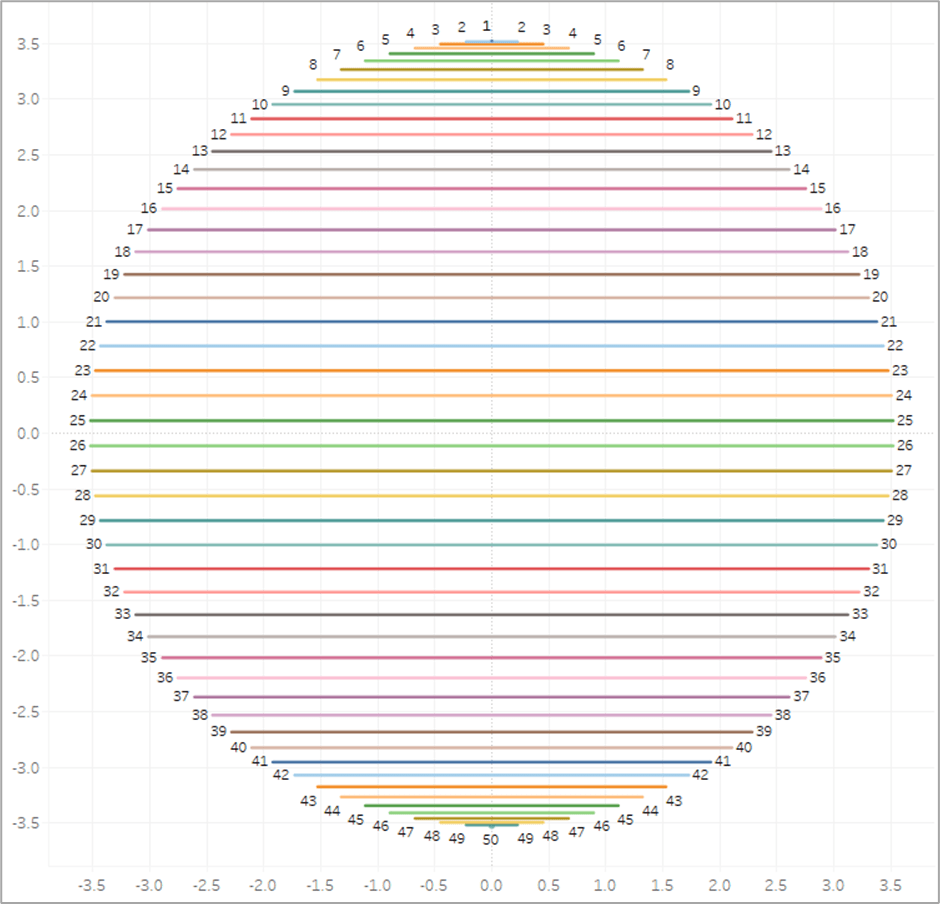
Screenshot showing how the lines connect to the mirror opposite position of the starting point

So that is the meat of this technique. Basically we are going to draw a bunch of perpendicular lines that go from one side of the circle to the mirror opposite side. Now for the rest of the calculations. Here are the [X] and [Y] calcs that I mentioned earlier that are used to actually plot the points around the circle using the [Radius] and [Position] inputs.

X = [Radius] * SIN(2 * PI() * [Position])

Y = [Radius] * SIN(2 * PI() * [Position])

And then finally our [Color] calculation is going to be exactly the same as Method #1. We’ll use the [Points] field to evenly calculate values between 0% and 100%.

Color = [Points]/[Max Points]

And now we are ready to build our view.

  • Similar to Method #1, if you are going to build a panel chart, drag the [Column] and [Row] fields to their respective shelves
  • Right click on [X] and drag to Columns shelf. When prompted, choose no aggregation
  • Right click on [Y] and drag to Rows shelf. When prompted, choose no aggregation
  • Change Mark Type to Line
  • Adjust the Size so the line thickness is at or near the minimum width
  • Change [Order] to a dimension and drag to Path
  • Change [Points] to a dimension and drag to Detail
  • Drag [Color] to color
  • Edit Colors and select your desired sequential palette
  • Use the parameter to rotate the circle if desired
  • Edit the X and Y axes so that the ranges are equal
    • It’s important to note that with this method, the X and Y axis ranges need to be equal for the circles to appear as perfect circles. If one axis range is longer/shorter than the other axis range, you will end up with ovals
    • It’s also important to note that when you place this worksheet on a dashboard, the Height and Width of the worksheet need to be equal to maintain it’s perfectly circular shape

When finished, your sheet should look something like this

Screenshot of Method 2 worksheet

If you are drawing large circles, you may need to add more densification records. Alternatively, you can increase the line thickness. But I have found that adding more records typically looks better than thicker lines, as the thickness of the lines can have an impact on the shape of the full circle. If you are drawing small circles, you can delete densification records. You can play around with the number of records you need until it looks just right.

Method 3: The Vertex Method

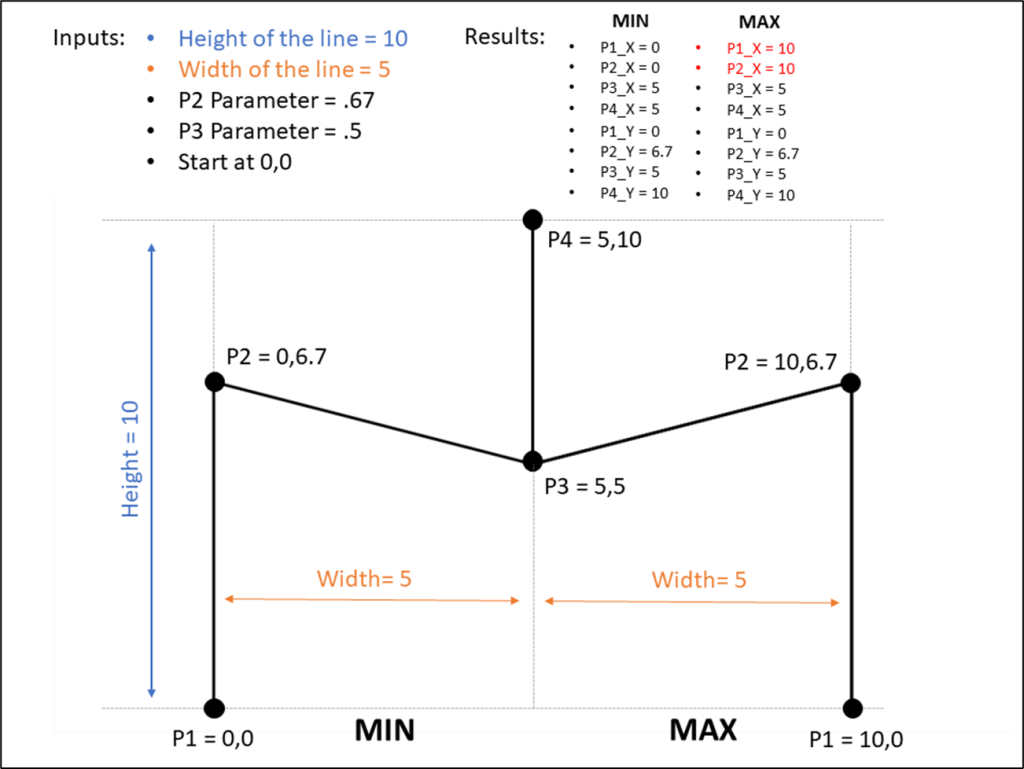
Now on to our final and most complicated method. There are a few differences between The Vertex Method and the Straight-Line Method, but the main difference is that our lines are going to use 3 points instead of 2. That 3rd point will allow us to control how the gradient appears (or where the “light” is coming from).

Setting up the data source for this method is exactly the same as Method #2. The only difference is that our Order table has 3 records instead of 2.

Screenshot showing the correct joins for Method 3

Similar to Method #2 we’re going to want to use parameters to “move” the light source, but in this case, we’ll have a lot more flexibility on how we can move it. We can move it up, down, left, right, basically anywhere. So we’ll use two parameters, one to move it up or down (adjusting the Y coordinate), and one to move it left or right (adjusting the X coordinate).

Screenshot of parameters used to move light source for Method 3

And then the start of this method is exactly the same as Method #2. We need to calculate our two inputs for the circle, the radius and the position. So our first few calculations are going to be identical.

Max Points = {MAX([Points])}

Radius = SQRT([Size]/PI())

Position_Base = (([Points]-1)/([Max Points]-1))

Position_Offset = [Position_Base]/2

Once again we’re calculating the Radius using the [Size] field, and then we’re calculating the Base position, and then dividing that by 2 to get all of our points evenly spaced along the right side of the circle. Now this is where the two methods begin to diverge. In Method #2, we were drawing perpendicular lines across the circle. With Method #3 the end of the line is going to be at the polar opposite of the start. Something like this.

Screenshot showing how the lines connect to points directly across the circle from start position

So our lines will start on one side of the circle, pass through the center, and then end at the point directly opposite of the starting point. And then what we’ll do is use our parameters to “move” that center. But we’re not there quite yet. First, let’s finish calculating our [Position] field.

Position = [Position_Offset] + IF [Order]=3 THEN .5 ELSE 0 END

So if [Order]=1 it’s going to use the [Position_Offset] value, which is the starting point, or the position along the right side of the circle. And then if [Order]=3, it’s going to add .5 (or 50%) to that value, which would be the position at the direct opposite side of the starting point. Next, let’s plug our Radius and Position into our X and Y calculations, but we’re going to call them [X_Base] and [Y_Base] since we’re not quite done with them.

X_Base = [Radius] * SIN(2 * PI() * [Position])

Y_Base = [Radius] * SIN(2 * PI() * [Position])

So for each of our lines, we need 3 sets of coordinates, or 6 values in total. We need X and Y values for the start of the line, the center of the line, and the end of the line. We’ve already done all the math we need to calculate each of those, but to make things easier, let’s build a few really simple calculations to isolate these. Let’s start with the X coordinate calculations.

Line_X_Start = [X_Base]

Line_X_Center = [Method 3: Gradient Center X] * [Radius]

Line_X_End = [X_Base]

I told you they were simple calcs. For the Start and End of our lines, we already calculated those values. Those will just be equal to that [X_Base] calc we built above. And the center of the line is going to use that parameter we built to move the “light” source left and right across the X axis. We just multiply that value, which is a decimal between -1 and 1, by the radius to determine how far to move it.

  • -1 would be all the way to the left.
  • 1 would be all the way to the right.
  • 0 would keep it in the center.
  • -.5 would move it halfway between the center of the circle and the left edge
  • and so on

Now, let’s build our Y coordinate calculations, which are nearly identical the X calcs above, except they’re going to use the [Y_Base] field, and the Y coordinate parameter

Line_Y_Start = [Y_Base]

Line_Y_Center = [Method 3: Gradient Center Y] * [Radius]

Line_Y_End = [Y_Base]

And then a couple of final calculations to bring all of these values together.

X = CASE [Order]
WHEN 1 then [Line_X_Start]
WHEN 2 then [Line_X_Center]
WHEN 3 then [Line_X_End]
END

Y = CASE [Order]
WHEN 1 then [Line_Y_Start]
WHEN 2 then [Line_Y_Center]
WHEN 3 then [Line_Y_End]
END

With this method, the center point of the lines is going to be where the light source “shines”. So if we were to leave those parameters at 0 & 0, the light would shine at the center of the circle and look similar to what we built with Method #1. Our individual lines would look like they did in the screenshot above (and the one on the left below). But if we adjust those parameters to say, .5 and .5, then the center point of the lines would move up and to the right (like the one on the right below). And once we add the gradient color to our lines, it will look like the light is shining from the upper right of the object.

Screenshot showing a comparison of how moving the center point affects the lines

It’s all starting to come together. We’ve calculated all of the points we need to draw the lines, we just need to add some color. This part is a little trickier than it was in the other two methods, but nothing we can’t handle. Similar to the other methods, we are going to use a value between 0 and 1 (or 0% and 100%) to assign our color. The main difference here is that we are going to use the length of each line segment to calculate that value. Each of our lines has two segments; start to center, and center to end. We’re going to use the Pythagorean Theorem to calculate both of those.

Each line segment is essentially the hypotenuse of a right triangle, so we can calculate that if we know the lengths of the other two sides of the triangle…which we do. Let’s isolate one of the lines from our screenshot above. Here is Line #1

image of isolated line #1

If it’s been a while since you’ve taken a Geometry class, which it certainly has for me, Pythagorean’s Theorem is a^2 + b^2 = c^2 where c is the hypotenuse. Now let’s look at this image again, but with the rest of our triangles drawn.

image of isolated line #1 with 2 sides added to each segment to create triangles

So for each of these triangles we can calculate the length of the “a” side, by subtracting the [Line_Y_Start] value (or [Line_Y_End] value depending on which segment you are measuring) from the [Line_Y_Center] value (result may be a negative number but the ABS of that value would equal the length). And we can get the length of the “b” side by subtracting the [Line_X_Start] or [Line_X_End] value from the [Line_X_Center] value. And with both of those, we can calculate the length of the “c” side, which is what we’re going to use in our color calculation.

First, let’s calculate the length of the first line segment, from the start of the line to the center of the line (which would be the red triangle in the screenshot above)

Line_Length_Start_to_Center = SQRT(SQUARE([Line_Y_Center]-[Line_Y_Start])+SQUARE([Line_X_Center]-[Line_X_Start]))

And to calculate the length of the second line segment, from the center of the line to the end of the line (the purple triangle above), it will be the same calculation but we’ll swap out the “Start” coordinates with the “End” coordinates.

Line_Length_Center_to_End = SQRT(SQUARE([Line_Y_End]-[Line_Y_Center])+SQUARE([Line_X_End]-[Line_X_Center]))

And then one last calculation called [Line_Length] to bring those values together and assign a value to each [Order] value. So if [Order]=1 we want to use the length of the first line segment (from start to center). If [Order]=2, we want to use a value of 0. And if [Order]=3, we want to use the length of the second line segment (from center to end). This may be confusing at the moment, but stick with me.

Line_Length = CASE [Order]
WHEN 1 then [Line_Length_Start_to_Center]
WHEN 2 then 0
WHEN 3 then [Line_Length_Center_to_End]
END

So let’s look at our example again with the Line Length value on Label

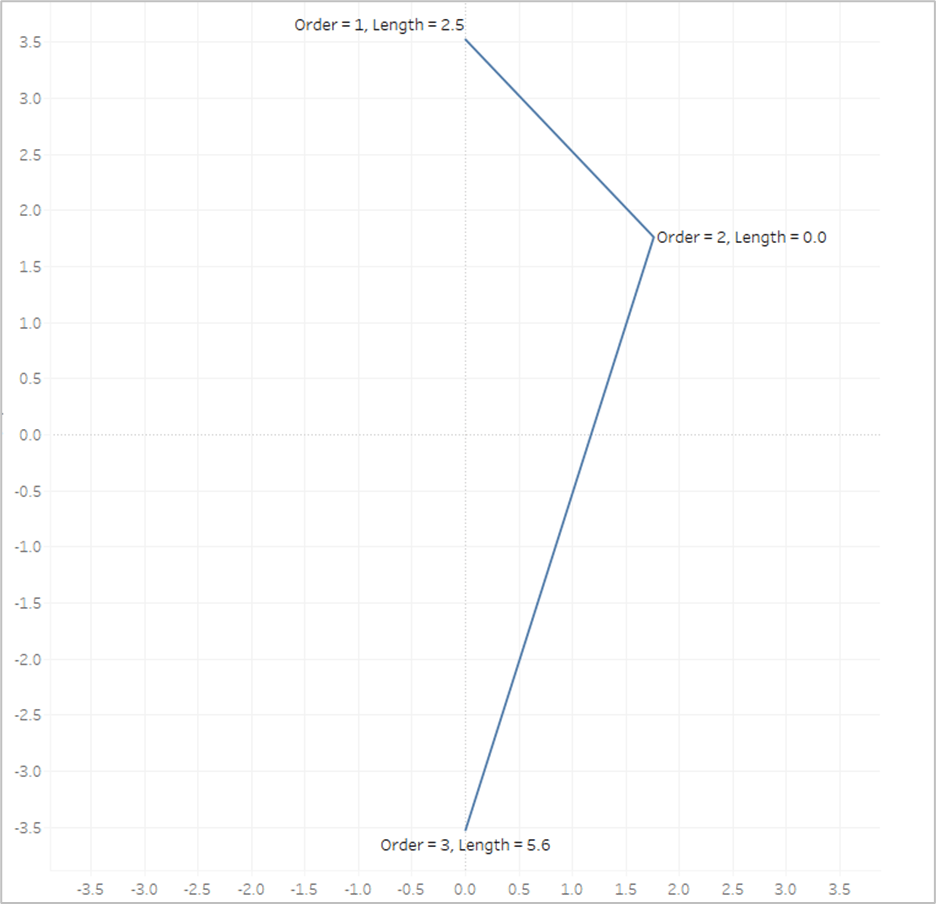
isolated image of line #1 with the Order and Length values labelled at each point

The length of the first line segment is 2.5, so we’ll assign that value to the 1st point, where [Order]=1. The length of the second line segment is 5.6, so we’ll assign that value to the last point, where [Order]=3. And when [Order]=2, we assign a value of 0. Now look what happens if we put that [Line_Length] field on Color and apply a sequential color palette.

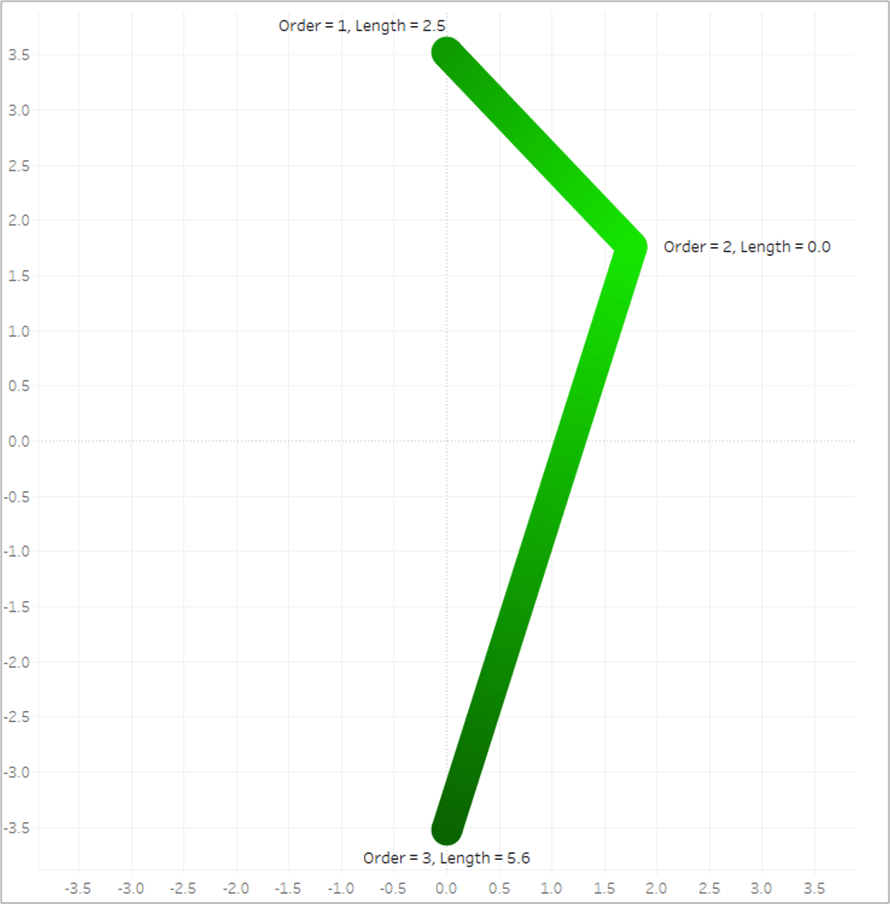
isolated image of line #1 with color gradient applied

Tableau assigns the lightest shade from our palette to the lowest number, which is 0, and assigns the darkest shade from our palette to the highest number, which is 5.6. And then it automatically generates all of the appropriate shades in between.

Now the last thing we need to do is to translate those numbers into percentages between 0 and 1. When we have different sized circles in the same view, they’re going to end up with different lengths, so we don’t want to use the actual length of each line, we want to use the length relative to the longest line for that circle. So the longest line will have a value of 1. And this will be our [Color] calculation.

Color = [Line_Length]/{FIXED [Dimension] : MAX([Line_Length])}

And now we are finally ready to build our view, which is going to be exactly the same as Method #2

  • Similar to Method #1 & #2, if you are going to build a panel chart, drag the [Column] and [Row] fields to their respective shelves
  • Right click on [X] and drag to Columns shelf. When prompted, choose no aggregation
  • Right click on [Y] and drag to Rows shelf. When prompted, choose no aggregation
  • Change Mark Type to Line
  • Adjust the Size so the line thickness is at or near the minimum width
  • Change [Order] to a dimension and drag to Path
  • Change [Points] to a dimension and drag to Detail
  • Drag [Color] to color
  • Edit Colors and select your desired sequential palette
  • Use the parameters to adjust the light source up/down/left/right
  • Similar to Method #2 you will need adjust the X and Y axis ranges so that they are equal (and make sure that the Height and Width of the worksheet are equal when placed on your dashboard)

When we’re done, our sheet should look like this

Screenshot of Method 3 worksheet

So this blog post is already much, much longer than I planned, but there is one last thing I want to touch on. What if you want to have multiple gradients in the same sheet?

Assigning Multiple Gradients

Use Map Layers. I’m not going to go through the entire process of building a view with map layers as that would double length of this already ridiculously long post. But that is how you would go about assigning multiple gradients. So in this last example, I’m going to use the [Group] field from our data source. It just has three different values, 3 of the records are assigned to Group A, 3 to Group B, and 3 to Group C.

I have 3 different groups that I want to assign 3 different colors, so I will create 3 different MAKEPOINT calculations.

Final_Group_A = if [Group]=’A’ then MAKEPOINT([X],[Y]) END

Final_Group_B = if [Group]=’B’ then MAKEPOINT([X],[Y]) END

Final_Group_C = if [Group]=’C’ then MAKEPOINT([X],[Y]) END

So each of these calculations will only return results if the records are in the associated group. The result will be null for anything outside of that group. Next, you just need to duplicate your [Color] field 3 times so you can assign a different palette to each Group

Color_Group_A = [Color]

Color_Group_B = [Color]

Color_Group_C = [Color]

And then you build the view exactly the same way, except that you add multiple layers, one for each of the Groups using the appropriate MAKEPOINT field. Instead of using the [X] and [Y] fields, it will use the generated latitude and longitude from those MAKEPOINT calcs. At the end, your view should look something like this.

Screenshot of Method 3 worksheet with multiple gradient colors applied

Alright, that was a long one. As always, I hope you enjoyed this post, and please let us know if you try out any of these gradient methods. We would love to see what you create with them!

Categories
How Did You Build That in Tableau? How-To's Tableau Techniques Totally Useless Charts

How did you build that in Tableau?

How did you build that in Tableau? That’s a question I get pretty frequently. If you look at my Tableau Public profile you may notice that most of my visualizations are pretty unique. And there’s good reason for that. Every visualization I build for Tableau Public, I try to do something I haven’t done before, and preferably, something I haven’t seen anybody else do. What I love about this approach is that I am continuously learning. I am constantly learning new techniques, combining those with other things I have learned along the way, and creating something new and, to me at least, something exciting. My favorite part about building these unique visualizations is figuring out how to do it. Sometimes it’s really challenging, but it’s also extremely satisfying when you finally figure it out and see your ideas come to life.

There are, of course, downsides to this approach. Inspiration and ideas are very hard to come by. I hear people all the time saying that they have so many viz ideas and not enough time to work on them. It’s the complete opposite for me. I will come up with one good idea every couple of months, and then spend days, weeks, sometimes months, figuring it out. That’s why I only have about 55 vizzes on my profile, even though I’ve been using Tableau Public consistently for about 4 1/2 years. That’s an average of about 12 per year. Some people seem to publish that many each month.

But it seems that every time I do publish something, I get at least a handful of messages on Twitter and LinkedIn asking “How did you build that?”, or often times, a much more general question “Can you tell/teach me how to build things like that?”

The first question is a little easier to answer, and could probably be done through a single blog post (which I plan to start doing in a new series with the same title “How did you build that in Tableau”). The second question is much harder to answer. It seems a lot of the time, people are looking for a silver bullet, one piece of advice, or one technique, that will allow them to build weird and crazy vizzes. And I really wish I had something like that to give them, but I don’t. As I mentioned earlier, every visualization I build is different. There isn’t a set technique or approach. But if I sit down and think about it, I do think there is a, at least somewhat, consistent process I go through with each build. And that’s what this post is about. This isn’t a technical walk-through, it’s more about the process. I will walk through a pretty basic example using that process, and if you’re interested in the calculations, please download the workbook here.

Step 1: The Idea

In my opinion, this is the hardest part. If you want to build something unique, you have to have a general idea of what it is you want to build. If you can imagine it, chances are there is a way to make it happen. And I am sending out an open invitation now: If you are taking the time to read this post, and you have a unique idea, but don’t know how to build it, feel free to reach out to me on Twitter or LinkedIn, and I will do my best to help you. As I mentioned earlier, I love trying to figure this stuff out.

Back to the idea. The idea gives you a starting point and something to work towards. But keep in mind that that idea is likely to change and evolve as you go through the rest of the process. I have very few examples of vizzes where the end result is exactly like what I had set out to build. It’s usually an iterative process. Come up with an idea, that idea doesn’t work the way you wanted it to work, but it sparks other ideas. Or maybe it did work, but along the way you got other ideas that would make it better. So the process I’m laying out here may not be completely sequential. You may find yourself back at this Step a few times before you build something you’re excited about.

Step 2: The Data

For me, this step and step 1 are interchangeable. I told you this process wasn’t always sequential right?

  • Sometimes I have an idea and then I go looking for the specific data I need.
  • Sometimes I come across a cool dataset, and then try to come up with ideas on how to visualize it.
  • Sometimes I have 0 ideas and I just browse Kaggle, Data.World, or Google and a dataset will spark a cool idea.
  • Sometimes I have an idea for a type of chart I want to try to build, and then go looking for any kind of interesting data I could use for that chart type.

There is no right way to do this. Think of it as writing a song. You need lyrics and you need music, but you don’t necessarily need to work on either of those things before the other. It could be a lyric or a melody that pops into your head and then you work around that. And chances are both the lyrics and the music are going to change when you start working them together.

So start with what you have and then go from there.

Step 3: The Plan

The next step is to start planning the build. You know what you want to build, but you need to figure out how to get there. If you want to start building truly unique visualizations in Tableau, you need to get comfortable with scatterplots. Nearly every single visualization on my profile is built using X and Y coordinates. I like to think of it like drawing, but more specifically, like drawing with connect-the-dots. That’s really all it is. It’s figuring out where to put the dots and how to connect them. With those two things figured out, you can draw anything you want in Tableau.

When I’m planning out my build, I like to break it out into smaller pieces. Let’s say we wanted to make this Smiley Face in Tableau, where would you start?

If I was trying to build this, I would start by figuring out the individual pieces that need to be built. In this case, I have one large yellow circle, two small black circles, and one curved black line. I don’t have to figure out how to build the entire thing at once, I just need to figure out how to build each piece and then figure out how to put them together.

I know how to draw circles in Tableau and I know how to draw curved lines in Tableau. I’m basically done. Not quite, but it’s a good start. Pretty much everything on my Tableau Public profile is built using some combination of circles and curved lines. The variety comes from combining those things in different ways. If you’re looking for more technical walk-throughs on how to build circles and curved lines in Tableau, check out the 3-part series on our blog:

Fun With Curves in Tableau Part 1: Circles
Fun With Curves in Tableau Part 2: Bezier Curves
Fun With Curves in Tableau Part 3: Sigmoid Curves

For my Smiley Face, I am going to use Techniques from Part 1 and Part 2 of that series. I’m going to draw 3 circles and 1 bezier curve. I’m not going to share all of the formulas here, so if you’re interested in following along, I would recommend reading Part 1 and Part 2, and downloading the example workbook here.

Step 4: The Data Structure

This part can be difficult. Figuring out how to structure your data so you can build the pieces you need to build. If you are trying to build something unique, chances are you will not be able to use your data as is. You’ll have to put some work into it, and chances are, you’ll revisit it and change it and re-arrange it as you go through the build. The technique I typically use, I like to call a “Stacked” Densification Table. If you’re not familiar with Densification, we’re basically creating additional records in our data source that we can use in our calculations. I am blowing up my data source, but I’m doing it with purpose.

For this example, I am going to use a data source with just a single record. If I wanted to draw more than one smiley face, I could add more. But here is my “Base” data.

Object IDObject NameSize
1Smiley Face 110

Now I’ll create my Densification Table. I’ll start by adding records to “draw” my first object; the Left Eye.

TypePoints
Left Eye1
Left Eye2
Left Eye3
Left Eye…
Left Eye20

I used 20 points, which works pretty well for smaller circles. The more points you add, the smoother your curves/circles will appear. Curves in Tableau are essentially a bunch of really short straight lines, so the more lines you have, the shorter those lines will be, and the smoother the curves will appear.

Now, in the same table, I’ll add another 20 records for the Right Eye.

TypePoints
Left Eye1
Left Eye…
Left Eye20
Right Eye1
Right Eye2
Right Eye3
Right Eye…
Right Eye20

Then I’m going to add 100 points for the body or face or whatever you want to call it. I’m using more points for this because the circle is much larger. Then I’ll add another 50 points for the mouth. The end result should be a table with 190 records; 20 for the Left Eye, 20 for the Right Eye, 100 for the Body, and 50 for the Mouth

The reason I like to set it up this way is that I can use different calculations and different techniques on each section, or Type, and then combine them later using a couple of simple calculations.

The last step in setting up my data source is to join these 2 tables using a physical join and a join calculation.

Step 5: The Build

Once I have my data structure in place, it’s time to start building. When I’m on Step 3 and planning out my build, I identify the individual pieces that need to be built. When I’m on Step 4 and building out my data source, I create the data I need to build each one of those individual pieces. And when I’m on Step 5 and actually building the viz, I work on each one of those pieces individually. I’m going to start with the body/face because it’s the biggest and because the position of all of the other pieces are going to rely on that piece.

The Build Part A: Building the Circles

My first step in building this circle would be to go to a new worksheet, and filter on Type = Body, because that’s the piece I’m working on first. My next step would be to build the calculations. If you looked at Part 1 of the Fun with Curves series, you’ll know that in order to draw a circle in Tableau, we need two inputs; the distance of each point from the center of the circle (the radius), and the position of each point around the circle.

In this case, I’m going to use the [Size] field from my data source for the size of the body/face circle. That value is going to represent the Area of the circle, so I’ll calculate the radius using that, and that will be the first input. Once I have that, and the Position input, I plug those into my X and Y calculations and build the circle. When I’m done, it will look something like this.

So far so good.

Next, I’m going to build the Left Eye. When I’m building something like this, I like to parametrize everything, so I can easily tweak the size and position of things, and so that the sizing will stay consistent, even if the values in the data change. And I always choose an “Anchor” value. Something I can use along with those parameters to calculate “relative” values for everything else. For this build, I’ll use the radius of the body/face as the “Anchor” because all of the other objects are going to go inside of (or really on top of) that main circle.

So in this case, I’ll build a parameter and set the value to .1 to start. Now, to calculate the radius for the eyes, I just multiply that parameter by the radius of the body/face. By using this technique, I can ensure that the radius of the eyes will always be 1/10th of the radius of the body/face. And I can also tweak that value to easily make the eyes larger or smaller.

My next step would be to repeat the process I used to build the body/face to build the left eye. I would go to a new worksheet, filter on Type = Left Eye, plug my eye radius and position into the X and Y calcs and build my circle. Then repeat for for the Right Eye.

The Build Part B: Placing the Circles

At this point, I would have 3 sheets and 3 sets of X and Y coordinates, one for each of the objects. Now I would bring them together with a couple of simple calculations called “Final_X” and “Final_Y”, which are just CASE statements that look at the TYPE field from my densification table and return the values of the appropriate X and Y fields that I have already calculated for each type.

Then I would go to a new sheet, filter on my 3 Types, and build the circles using those “Final” X and Y fields.

When I’m done, it would look something like this.

Hmmm, that looks exactly like the “Body” worksheet. One thing to always keep in mind when layering these objects is how Tableau sorts them. In this case, Tableau sorted the “Types” alphabetically, so the Body is in front of the Left Eye and Right Eye. So next, I would click on the color legend and drag Body to the bottom and the objects will sort correctly. With a lot of objects, sometimes this sorting piece can become pretty complicated. Once sorted, it would look something like this.

Now unless I was building a cyclops smiley face, this still doesn’t look right. As it stands now, all of my circles have the same starting point. They all start at 0,0 and build around that. I want the Body to start at 0,0 but I need to offset the eyes to get them in the right position. Basically, the eyes need new starting points.

Offsetting these values is really easy. If you want to move something up? Add a positive value to it’s Y coordinate. Want to move something down? Add a negative value to it’s Y coordinate. To the right? I’m sure you’ve guessed it, add a positive value to the X coordinate.

This is something I struggled with early on, but once I understood it, it became really simple. Basically, what I am trying to do is to create a new starting point for each of these circles, instead of starting them at 0,0. And to do that, all I have to do is add those new starting coordinates directly to the X and Y calcs for each of the circles, and all of the other points I have already calculated to form those circles, will move accordingly.

Once again I would use parameters to determine how far to move the circles, one for moving them up and down, and one for moving them left and right. Then it’s just a matter of multiplying those parameters by my “Anchor” value, the radius of the body/face, to get the actual values and then adding (or subtracting) those values to the X and Y fields for the Left and Right Eye.

After moving the eyes, I have something like this.

It’s starting to look pretty good, but, in my opinion, those eyes look a little too small, a little bit too spread out, and just a touch too high. This is why I use parameters. Now I can easily tweak all of my parameters to change the look of it.

This looks much better, but now I notice another problem. Now that I made the eyes a little bigger, I can really see the lines instead of a smooth curve. This happens to me pretty frequently, but there is an easy fix. I go back to my data source and add more rows to the “Stacked” Densification table for the Left Eye and the Right Eye. If I increase that count to 40 (from 20), it looks much better. No more jagged lines.

The Build Part C: Building the Line

Now for the mouth. Like most things in Tableau, there are a couple of ways to accomplish this, but I am going to use a bezier curve. And I am going to start on this the same way I started with the circles, with a fresh worksheet filtered on the object I’m working on (in this case [Type] = Mouth).

To draw a bezier curve, I need the coordinates for 3 points…the Start of the line, the End of the line, and the Mid-point. And, just like I did for the eyes, I’m going to create some parameters so I can play with how the mouth looks. I’m going to create a total of 3 parameters; 1 for the width of the mouth, one for the vertical starting position of the line, and one for how far down the line dips. And again, just like I did for the eyes, I’m going to multiply these by the “Anchor” value to calculate the coordinates.

Once I have all of my calculations and I plug them into the X and Y calculations for bezier curves, I have something like this.

Now I have my curved line, but I can’t really tell what it’s going to look like until I place it on my Smiley Face. So I’ll do that next.

The Build Part D: Placing the Line

Now this part is a little tricky. I have my “Final_X”and “Final_Y” calcs that I used to bring the three circles together in the same view. But now I have 2 different mark types; Polygon for the Circles, and Line for the Mouth. So here is a technique I use to bring different Mark Types together on the same view.

I need to create a Dual Axis chart, so I can assign a different Mark Type to each axis. So Instead of “Final_X”, I would build “Final_X_Circle”, which would include all of my Circle X calculations, and “Final_X_Line”, which would include all of my Line X calculations. For each of those Fields, the result would be populated for the included “Types” and NULL for all other Types.

Then, I would add all of the Types to the “Final_Y” calculation. If I built separate calculations for the Mark Types here, I would not be able to layer them together in the view.

So I end up with a common measure for the Y axis, and two different measures for the X axis

Now I can create a dual axis chart, and set the appropriate mark type for each of my Types. With a few more minor tweaks, I have something like this.

Now, just like I did with the eyes, I can play around with the parameters to get the smile to look how I want.

Step 6: Ideate & Iterate

At this point, I have built what I set out to build, so I should stop right? As I mentioned earlier, as I’m working through this process, I usually have other ideas to try out. Now that the foundation is built, how can I make it better?

What if I added another record to my “Base” data?

What if I added 100 records and made a 10×10 panel chart?

What if I put some real data behind this? Since I’m working with Smiley Faces, how about data from the World Happiness Report? What if I made them all the same size, but used color for the Happiness Score?

That’s looking better. But maybe the faces with the lower scores should be frowning instead of smiling. What if I could use the score to control the shape of the mouth too?

Now what if I used population on Size?

Hmmm, that doesn’t really work. Most of those faces are way too small. I would need to make them all bigger, but I can’t really do that with a panel/trellis chart. But what if I made this into a Packed Bubble Chart and limited it to the 50 largest Countries?

Ooohh, now we’re getting somewhere. Now what if I grouped the countries by Continent?

That’s it! That’s the one. Now it may seem like a huge leap going from a single smiley face to this, but it was actually a really easy update. I set up everything with parameters and used “Anchor” values, so no matter how many records I added to my data source, I would have a smiley face, with the correct proportions for the features, for every record.

And moving from a Panel Chart to a Packed Bubble chart was easy as well. CJ Mayes has a really great tutorial on Circular Packing, which is what I used. The output of that process is a file with an X coordinate, a Y coordinate, and a Radius for each circle. That means I could take what I had already built, and just add the X coordinate to my “Final” X calcs, and the Y coordinate to my “Final” Y calc to give all of my circles a new starting point. Then I swapped out the Radius calc I had used for the body/face with the one in the output. Because everything else I built was Anchored to that Radius value, everything updated and moved automatically.

Step 7: Final Touches

Now that I have built something I’m happy with, it’s time to finish off the design. I typically don’t spend a lot of time on this. If you look at my profile you’ll notice that nearly all of my vizzes are a single unique chart, with a light background, a title, some text, and some ways to interactive with the viz. I’m not a great designer, so I try not to put too much effort into the design. Also, I spend a lot of time building those charts, and I want those to be the focal point.

If I was going to publish this, it would probably look something like this.

I would play around with the design of the chart a little bit, add a Title and Subtitle, and some text describing the chart. If I was going to publish this I would also probably add some kind of interactivity to highlight specific countries to make them easier to find, and maybe bring this into Figma to add some labels for the continents. But, since I’m not publishing it, this seems like a good place to stop.

Wrap-Up

I hope you found this helpful. This is the exact process I would have gone through if I was trying to build a Smiley Face in Tableau. I know it is, because I wrote this post as I was building it. This was my actual process from trying to build this:

To actually building this:

As I mentioned earlier, there isn’t a single, universal technique that will let you build anything and everything in Tableau, but there is a process you can follow that may help you. I know it helps me. The most important parts of that process, in my opinion, are Step 1, Step 3, and Step 6.

Coming up with unique ideas is tough, but you have to know what you want to build, or at least attempt to build, before you can start building it. If you don’t have an idea, start looking for some interesting datasets, and then think of unique ways you can visualize it.

And then you have to plan. If you just sit down with an idea and start writing calculations, maybe you’ll get there, maybe you won’t, but your chances will increase significantly if you have a plan. These builds can be overwhelming, so you’ll want to break it down into smaller, more manageable pieces. Work on those pieces individually, and then start bringing them together. I recently published a few games, and although the goal of those was completely different than one of my visualizations, the process was exactly the same. I broke it down into smaller pieces. How would I build and position each of the pieces? What are the rules for the game? What has to happen each time a user clicks? What restrictions should there be when it’s time to make a move? How would a winner be determined? I sat down and thought through all of these questions before I ever opened Tableau and I came up with a plan for addressing each of them.

And then once you have something built, experiment with it. Every change you make might not be an improvement, but it’s still worth trying. Maybe you’ll love it, or maybe it’ll spark other ideas you can experiment with. Or maybe you’ll have to hit undo 100 times. It doesn’t matter, try it anyways.

If you use this process for a new visualization, or if you have your own process, please reach out and tell me about it. And, as I mentioned earlier, if you have a unique viz idea but can’t figure out how to build it, reach out and I’ll do my best to help. And keep an eye on our blog for the new series “How Did You Build That in Tableau”, where we’ll walk through the process of how we built specific vizzes.

Categories
How-To's Totally Useless Charts

Totally Useless Charts & How to Build Them – Curvy Bump Chart with Bars

Ok, so this chart may not be totally useless, but I’m going to keep it in this category because it’s something I would never build at work. I love a good bump chart, but there is one major limitation with traditional bump charts. They are great for displaying changes in rankings over time, but what about the data driving those rankings. How much has a value changed from one period to the next? How much separation is there between #1 and #2? Surely a bar chart would be better for that type of insight right? Well, in this tutorial, we’re going to walk through building a chart that combines all of the benefits of bump charts and bar charts, and with some fancy curves to boot.

I’m sure I’m not the first to build this type of chart, but the first time I used it was in my 2020 Iron Viz Submission to show Happiness Scores by continent over time.

An image showing an example of this chart type used in a previous visualization

Looking back, there are definitely some things I would change about this, and I’m going to address those in the chart we are about to build. The data we’re going to be using for today’s walkthrough is on Browser Usage Share over the last 13 Years (showing usage at every 3-year increment). You can find the sample data here, and the sample workbook here. This is what we’re going to build.

An image of a curvy bump chart with bars displaying the percentage of usage share for different browsers

Building Your Data Source

Our data source (on the Data tab in the sample file) contains 5 fields. We have a Time Period (our Year field), a Dimension (the Browser), and a Value (the Share of Usage). There are also 2 calculated fields in this file. These could be calculated in Tableau using table calcs, but because of the complexity of some of the other calculations, we’re going to make it as easy as possible and calculate these in the data source. The [Period] field, is just a sequential number, starting at 1, and it is related to the Date field. The [Rank] field is the ranking of each Browser within that period.

On the next tab (Densification), we have our densification data. There is a [Type] field, which will allow us to apply different calculations, in the same view, for our bars and our lines. There is a [Points] field, which will be used to calculate the coordinates for all points for both the bars and the lines. And there is a [T] field, which will be used to draw the sigmoid curves connecting each of the bars.

If you are building this with a different set of data, just replace the Date, Browser, and Share fields in the Data Tab. The calculated fields should update automatically.

Now for joining this data. We are going to do two joins in the Physical layer in Tableau. We are going to do a self-join on the Data to bring in the rank for the next period, and we’re going to join to our densification data using a join calc.

To get started, connect to the Sample Data in Tableau and bring out the Data table. Then double-click to go into the physical layer. Now drag out the Data table again. First, join on [Browser]. Then create a join calculation on the left side of the join, [Period]+1 and join that to [Period]. Then set it as a Left Join. It should look something like this.

An image demonstrating a self-join

Now bring out your Densification table, and join that to the Data Table using a join calculation, with a value of 1 on both sides of the join. Like this.

An image demonstrating a join to a densification table

Now go to a new worksheet and rename the following fields.

Period(Data1) change to Next Period

Rank(Data1) change to Next Rank

I would also recommend hiding all other fields from the Data1 table to avoid confusion later on.

Building the Bars

To build the bars in this chart, we are going to use polygons. So we’ll need to calculate the coordinates for all 4 corners for each of our bars. Let’s start with Y, since that one is a little easier.

The first thing we are going to do is create a parameter to set the thickness of our bars. Create a parameter called [Bar Width], set the Data Type to Float, and set the Current Value to .75.

We are going to use the [Rank] field as the base for these calculations. Then, we are going to add half of the [Bar Width] value to get the upper Y values, and subtract half of the [Bar Width] value to get the lower Y values. Let’s create a calculated field for each of those, called [Y_Top] and [Y_Bottom].

Y_Top = [Rank]+([Bar Width]/2)

Y_Bottom = [Rank]-([Bar Width]/2)

If you look back at our Densification table, we have 4 points for the Bars, one for each corner. The order of these doesn’t really matter (but it is important that you are consistent when calculating the X and Y coordinates). In this example, we are going to start with point 1 at the bottom left, point 2 at the top left, point 3 at the top right, and point 4 at the bottom right. Like this.

An image highlighting the 4 points of a rectangle, starting in the bottom left, and ending at the bottom right

Now we’ll create a calculated field that will calculate the Y value for all 4 points. Call this [Bar_Y]

CASE [Points]
WHEN 1 THEN [Y_Bottom]
WHEN 2 THEN [Y_Top]
WHEN 3 THEN [Y_Top]
WHEN 4 THEN [Y_Bottom]
END

Now we need to do something similar for our X values, but instead of calculating the top and bottom positions, we need to calculate the left and right positions. Here, we will use the [Period] field as the base (which will also be the left side value), and then add the length of the bar to get the right side values.

If you remember from earlier, our [Period] field is a sequential number, starting at 1, and in this example, ending at 6. So each period has a width of 1. But we don’t want our bars going all the way up to the next period, so we’ll use a parameter to add a little spacing. Create a parameter called [Period Spacing], set the Data Type to Float, and set the Current Value to .3.

With this parameter and it’s current value, our largest bar in the chart should have a length of .7 (or 1 minus .3). All of our others bars should be sized relative to that. But first, we need to find our max value, which we will do with a Level of Detailed Calculation called [Max Value].

Max Value = {MAX([Share])}

And now we’ll calculate the length of all of our bars by dividing their [Share] by that [Max Value], and then multiplying that by our maximum bar length of .7 (or 1 minus .3). Call this calculation [Bar Length]

Bar Length = ([Share]/[Max Value])*(1-[Period Spacing])

Now, similar to what we did for our Y values, we are going to create calculated fields for [X_Left] and [X_Right]. [X_Left] will just be the [Period] value, and [X_Right] is just the [Period Value] plus the length of the bar, or [Bar Length]

X_Left = [Period]

X_Right = [Period]+[Bar Length]

Let’s take another quick look at the order of points.

An image highlighting the 4 points of a rectangle, starting in the bottom left, and ending at the bottom right

So Point 1 should be the left value, Point 2 should also be the left value, Point 3 should be the right value, and Point 4 should also be the right value. So let’s use this to calculate [Bar_X].

CASE [Points]
WHEN 1 THEN [X_Left]
WHEN 2 THEN [X_Left]
WHEN 3 THEN [X_Right]
WHEN 4 THEN [X_Right]
END

Now let’s test out our calculations so far.

  • Drag [Type] to the filter shelf and filter on “Bar”
  • Right click on [Bar_X], drag it to Columns, and when prompted, choose [Bar_X] without aggregation
  • Right click on [Bar_Y], drag it to Rows, and when prompted, choose [Bar_Y] without aggregation
  • Right click on the Y axis, select Edit Axis, and then click on the “Reversed” checkbox
  • Change the Mark Type to “Polygon”
  • Right click on [Points], drag it to Path, and when prompted, choose [Points] without aggregation
  • Drag [Browser] onto Color
  • Right click on [Period], drag it to Detail, and when prompted, choose [Period] without aggregation

When finished, your view should look something like this.

An example of what the polygon bars should look like at this point

Now onto our lines!

Building the Lines

Before starting this section, I would recommend taking a look at Part 3 of the Fun With Curves Blog Series on Sigmoid Curves.

The first calculation we need is [Sigmoid]. As I mention in the post above, this is a mathematical function that will appropriately space our Y values.

Sigmoid = 1/(1+EXP(1)^-[T])

Now, let’s calculate the Y coordinates, which in this case, we’ll call [Curve]. To calculate this, we’re going to use the [Rank] field as our base. Then we’re going to calculate the total vertical distance between the rankings for one period and the next and multiply that by our Sigmoid function to get the appropriate spacing. In the calculation below, the first part is optional, and is included only for labelling purposes. For the final period, there is no [Next Period], so this value would end up being blank, resulting in no label in our final step. So feel free to skip it and just use the portion between ELSE and END if you’re not going to label the bars.

Curve = IF [Period]={MAX([Period])} THEN [Rank] ELSE [Rank] + (([Next Rank] – [Rank]) * [Sigmoid]) END

The [Curve] calculation will give us our Y coordinates for all of points, so we just need X. Before we do that, let’s create one more Parameter that will be used to add a little spacing between the end of the bar and the start of our line (so the line doesn’t run through the label, making it difficult to read). Call this Parameter [Label Spacing], set the Data Type to Float, and set the Current Value to .15.

Now, we’re going to create a calculation for the start of our lines, which will be the end of the bar + spacing. I’ve also added a little additional logic so that the amount of spacing will depend on whether the label is 1 or 2 characters. If the [Share] value is less than 10 (1 character), we’ll multiply the [Label Spacing] by .7, and if it’s over 10, we’ll use the [Label Spacing] as is. Call this calculation [Line_Start].

Line Start = [X_Right]+IF [Share]<10 THEN [Label Spacing]*.75 ELSE [Label Spacing] END

Our next calculation will calculate the horizontal spacing for our points. In our Densification table, we have 25 Points for the lines, and this calculation will be used to evenly space those points between the end of one bar (plus the spacing for the label), and the start of the next bar. Call this calculation [Point Spacing].

Point Spacing = if [Period]={MAX([Period])} THEN 0
ELSE ([Next Period]-[Line_Start])/({COUNTD([Points])-1})
END

Similar to the [Curve] calculation, the first part of this IF statement is only for labelling purposes. If you’re not going to label your bars, you can just use the portion of the calculation between ELSE and END.

And now, with our [Line_Start] and our [Point_Spacing] fields, we can calculate the X coordinates for all 25 of points of each line. Call this [Line_X].

Line_X = [Line_Start]+(([Points]-1)*[Point Spacing])

Now let’s test out our calculations.

  • Drag [Type] to the filter shelf and filter on “Line”
  • Right click on [Line_X], drag it to Columns, and when prompted, choose [Line_X] without aggregation
  • Right click on [Curve], drag it to Rows, and when prompted, choose [Curve] without aggregation
  • Right click on the Y axis, select Edit Axis, and then click on the “Reversed” checkbox
  • Change the Mark Type to “Line”
  • Right click on [Points], drag it to Path, and when prompted, choose [Points] without aggregation
  • Drag [Browser] onto Color
  • Right click on [Period], drag it to Detail, and when prompted, choose [Period] without aggregation

When finished, it should look something like this.

An example of what the curved lines should look like at this point

Now all that is left to do is to combine our “Bar” calculations and our “Line” calculations in the same view.

Building the Final Chart

Because of the way we set up our Densification table, we have separate points for each of our bars and each of our lines. With just a few more simple calculations, we can bring everything together in the same view.

We want to leverage two different Mark Types in this view, Bar and Line, so we’ll need to create a Dual Axis chart. In order to do this, we’ll need a shared Field on either the Column or Row shelf, and then we’ll need separate fields for our Lines and Bars on the other Shelf. In this example, we’ll create a shared field for Rows, called [Final_Y].

Final_Y = IF [Type]=”Bar” THEN [Bar_Y] ELSE [Curve] END

This calculation is pretty straight forward. For our “Bar” records (where the [Type] field in our densification table = Bar), use the Y coordinates for our Bars, [Bar_Y]. Otherwise, use the Y coordinates for our Lines, [Curve]. We’re going to do something similar for X, but we need separate calculated fields for the Bars and Lines to create our Dual Axis. We’ll call these [Final_X_Bar] and [Final_X_Line].

Final_X_Bar = IF [Type]=”Bar” THEN [Bar_X] END

Final_X_Line = IF [Type]=”Line” THEN [Line_X] END

And now we’ll use those 3 calculated fields to build our final view. Let’s start with the Bars.

  • Right click on [Final_X_Bar], drag it to Columns, and when prompted, choose [Final_X_Bar] without aggregation
  • Right click on [Final_Y], drag it to Rows, and when prompted, choose [Final_Y] without aggregation
  • Right click on the Y axis, select Edit Axis, and then click on the “Reversed” checkbox
  • Change the Mark Type to “Polygon”
  • Right click on [Points], drag it to Path, and when prompted, choose [Points] without aggregation
  • Drag [Browser] onto Color
  • Right click on [Period], drag it to Detail, and when prompted, choose [Period] without aggregation
  • Drag [Type] to Detail

And now we’ll add our lines.

  • Right click on [Final_X_Line], drag it on to Columns to the right of [Final_X_Bar], and when prompted, choose [Final_X_Line] without aggregation
  • Right click on [Final_X_Line] on the Column Shelf and select “Dual Axis”
  • Right click on either X axis and choose “Synchronize Axis”
  • On the Marks Card, select the [Final_X_Line] Card
  • Change the Mark Type to “Line”
  • Remove “Measure Names” from Color
  • On the Marks Card, select the [Final_X_Bar] Card and remove “Measure Names” from Color
  • Right click on the Null indicator in the bottom right corner and select “Hide Indicator”

When finished, the chart should look something like this.

An example showing what the bars and curved lines together should look like at this point

Now for the final touches

Formatting the Chart

All of these steps are optional and you can format the chart however you’d like. But these are some of the adjustments that I made in my version.

First, I added labels. You can’t label Polygons, so our label has to go on the [Final_X_Line] Card. So click on that Card and then drag the [Share] field out onto Label. Then click on Label and under “Marks to Label”, choose “Line Ends”, and under “Options”, choose “Label start of line”. Then, because the values in my [Share] field are whole numbers instead of percentages (ex. 20% is listed as 20 instead of .2), I added a “%” to the end of the label (by clicking on the Text option) and formatted the field as a Whole Number. The Label options should look like this

An image showing the described Label options

Those Label options, along with the [Label Spacing] parameter we created earlier, should give you a pretty nice looking label between the end of your Bar and the start of the Line.

Next, I cleaned up and formatted the Axis. For the X axis, I set the Range from .9 to 7 and then hid both of the X axes. For the Y axis, I set the range from .5 to 9.5, and set the Major Tick Interval to 1. I then removed the Axis title and made the text a bit larger. I also used a Custom Number Format, so I could put a “#” sign before the Ranking number. Like this.

An image showing the Custom Number formatting with "#"0

Then I added some Grid Lines on Columns to give the Bars a uniform starting point, and some really faint Grid Lines on Rows to make it easier to track the position for any given Bar.

Finally, on the dashboard, I added a Title, I added a second simple worksheet to display the Years, and added a Color Legend that can also be used to Highlight any of the Browsers. And here’s the final version.

An image of the final visualization

As always, thank you so much for reading, and if you happen to use this tutorial or the template, please reach out and share what you built with us. We would love to see it! Until next time.

Categories
How-To's Totally Useless Charts

Totally Useless Charts & How to Build Them – “Hand-drawn” Bar Charts

Welcome to our 2nd installment of Totally Useless Charts & How to Build Them, where we do…exactly what the name implies. Look at some totally useless charts and walk through, step by step, how to build them. If you missed the first installment, the goal of this series isn’t necessarily to teach you how to build these specific useless charts, but more to talk through the techniques, the approach, and the thought process behind each chart, so you can apply those concepts to your own custom charts.

In this installment we’re going to learn how to build “hand-drawn” bar charts in Tableau. These of course aren’t actually hand-drawn, but using some interesting techniques, and a lot of random numbers, we can kind of make them look that way. If you would like to follow along, you can download the workbook here, and the data here.

“Hand-Drawn” Bar Charts

First, let’s look at an example of what we’re talking about. Here is a viz that I published recently about relationships on the show “The Office”. You can check out the interactive viz here.

My goal was to make the entire viz look like an office desk belonging to everyone’s favorite receptionist/office manager, Pam Halpert. To do that, I had to make all of the visualizations appear to be “hand-drawn”, including the bar charts. Let’s zoom in one those.

Here we have two different bar charts, one for the Longest Relationship, and one for the Most Time in Relationships (by number of episodes). Today we’re going to be using different data, but the goal is still the same…build some bar charts that look “hand-drawn”.

Building Your Data Source

Let’s start with our data. For this example we’re going to look at the top 10 highest grossing films of all time. If you downloaded the sample data, you can find these in the “Data” tab.

Next, we need to do some densification. The first thing we need to do is to create a record for every line needed in each bar. If you look at one of these bars closely, you’ll see that it’s actually made up of a bunch of lines…one outer line (orange), and a number of cross lines (blue).

So we are going to densify our data with our first densification table, called “Lines” in the sample data. In this table, we have 1 record for our Outer Line, and 50 records for our Cross Lines

Then we’re going to join our “Data” table, and our “Lines” table using a join calculation with a value of 1 on each side.

But we’re not quite done yet. Now we have a record for each of our lines, but each of those lines is made up of multiple points. Our “Outer Line’ is made up of 4 points, and each of our “Cross Lines” is made up of two points

So we’re going to use one more densification table to create additional records for each of these points, for each of the lines. This table is called “Points” in the sample data

And we’re going to join this to our “Lines” table on the [LineType] Field.

Now for each of our 10 films, we have 4 records for our “Outer Line” and 100 records for our “Cross Lines”, 2 for each of the 50 lines in the “Lines” table.

Drawing the “Outer Lines”

Now we have our data, let’s start building our Totally Useless Chart. We’re going to start with the Outer Lines. To do this, and to make it a bit dynamic so you can play around with how the chart looks, we’re going to build 4 Parameters. Each of these is going to have a Data Type of “Float” and the Default values are below

  • Bar_Width = .6 (used for the height of each bar and the spacing between the bars)
  • Scale_Bar_Outer_Height = .03 (used along with a random number to jitter points vertically)
  • Scale_Bar_Outer_Length = .1 (used along with a random number to jitter points horizontally)
  • Cross Lines = 50 (used to limit the number of cross-lines in each bar. This is optional)

Next, we’ll start building our calculations. The first, and arguably most important of these calcs is going to be our [Jitter] calculation. We want a random number between -1 and 1. The Random() function will give us a random number between 0 and 1, so we can modify that by multiplying the random number by 2 and then subtracting 1 (so a random number of .6 would become .2, and a random number .4 would become -.2)

Jitter = Random()*2-1

Next, we need to calculate the length of each of our “bars”. We’re going to do this by comparing each value to the maximum value and then multiplying it by the Max Length, which in our case will be the number of “Cross” lines we have. So the highest grossing film, Avatar, will have a length of 50, since we have 50 “Cross” lines. ((2.847B/2.847B)*50). Number 10 on the list will have a length of around 26.6 ((1.515B/2.847B(*50). So first, let’s calculate our Max length.

Max Length = {MAX([Line ID)}

Next, we’ll want to divide the Box Office Gross for each movie by the value for the highest grossing movie. The result of this will be a percentage which we’ll then multiply by our [Max Length] field to get our [Outer Bar Length]

Outer Bar Length = ([Box Office Gross]/{MAX([Box Office Gross])})*[Max Length]

Now, we need to calculate the X and Y coordinates for the 4 points of each “Outer Line”. So under normal circumstances, point 1 and point 4 would start at 0, and point 2 and point 3 would just be the [Outer Bar Length]. So if you connected those points, it would start at 0 for point 1, go to the end of the line for point 2, stay at the end of the line for point 3, and then return to 0 for point 4. But we want this to look “hand-drawn”, and if I was drawing bar charts by hand, there is no way they would align that neatly. That’s where our [Jitter] and “Scale” parameters come in.

Outer_Bar_X

CASE [Points]

WHEN 1 then 0+([Jitter]*[Scale_Bar_Outer_Length])

WHEN 2 then [Outer Bar Length]+([Jitter]*[Scale_Bar_Outer_Length])

WHEN 3 then [Outer Bar Length]+([Jitter]*[Scale_Bar_Outer_Length])

WHEN 4 then 0+([Jitter]*[Scale_Bar_Outer_Length])

END

We just want to move these points slightly to get that “hand-drawn” effect, which is why we are using the “Scale” parameters. For that first point, if we just did 0+[Jitter], that value could fall anywhere between -1 and 1, which is a pretty significant shift. But using the [Scale_Bar_Outer_Length] parameter, we can increase that value to get more jitter, or decrease the value to get less jitter. Using a value of .1 in the parameter, means that the value for that first point would now fall somewhere between -.1 and .1.

Next, we need to calculate our Y coordinates for those same 4 points. Again, under normal circumstances, for point 1 we would add half of the bar width to our starting point (the middle of the bar), same for point 2, and then for points 3 and 4, we would subtract half of the bar width from the starting point. So, along with the X coordinates, it would look something like this.

This is where the [Bar_Width] parameter comes into play. We need to know how thick these bars should be. We’re using the [Rank] field as our starting point, so the first bar will start 0,1, the second bar will start at 0,2, and so on. But we don’t want the bars to overlap, or be right up against each other, so we can control that with the parameter. A larger value in this parameter will result in wider bars and less spacing, a smaller value will result in skinnier bars, and more spacing. A value of 1 will result in no spacing between the bars.

Also, similar to the calculation for the X coordinates, we are using that [Jitter] field along with a “Scale” parameter to control how much jitter there will be. So a larger number in the [Scale_Bar_Outer_Height] parameter will result in more vertical jitter, and a lower number will result in less. Here is the calculation for the Y coordinates.

Outer_Bar_Y

CASE [Points]

WHEN 1 then [Rank]+([Bar_Width]/2)+([Jitter]*[Scale_Bar_Outer_Height])

WHEN 2 then [Rank]+([Bar_Width]/2)+(([Jitter]*[Scale_Bar_Outer_Height])/2)

WHEN 3 then [Rank]-([Bar_Width]/2)+(([Jitter]*[Scale_Bar_Outer_Height])/2)

WHEN 4 then [Rank]-([Bar_Width]/2)+([Jitter]*[Scale_Bar_Outer_Height])

END

Now we have all of the calculations needed to draw our “Outer” lines. So let’s do that

  • Drag [Line Type] to the filter shelf and filter on “Outer Lines”
  • Right click on [Outer_Bar_X], drag it to Columns, and when prompted, choose [Outer_Bar_X] without aggregation
  • Right click on [Outer_Bar_Y], drag it to Rows, and when prompted, choose [Outer_Bar_Y] without aggregation
  • Change the Mark Type to “Line”
  • Right click on [Rank], select “Convert to Dimension” and then drag [Rank] to Detail
  • Right click on [Points], drag it to Path, and when prompted, choose [Points] without aggregation
  • Right click on the Y-axis, select “Edit Axis”, and check the box labelled “Reverse” under Scale

When that’s finished, you should have something that looks like this. There are 10 “bars”, with all 4 points in each bar slightly jittered to give it that “hand-drawn” look.

Next, we need to add the “Cross Lines”

Drawing the “Cross Lines”

To help understand the approach we’re going to take, think about taking each of these bars and breaking them into individual segments. So, for example, our first bar has a length of 50 (think back to the Max Length calculation). So we want to break that into 50 individual segments and draw a diagonal line from the top left of the segment to the bottom right of the segment.

The image above is roughly what it would look like if we draw perfect lines across those segments. But we don’t want perfect lines. We want “hand-drawn” lines. So we’re going to leverage our [Jitter] field and our “Scale” parameters once again.

So let’s build our X and Y calculations. Remember when we built our data source, for our “Cross Lines”, we needed two points, 1 and 2. So Point 1 is going to start the line at the top left of our segment, and Point 2 is going to end the line at the bottom right of our segment. Here is the calculation

Cross_X = if [Points]=1 then [Line ID]-1 + ([Jitter]*[Scale_Bar_Outer_Length]*2) else [Line ID]+([Jitter]*[Scale_Bar_Outer_Length]*2) END

Here we are calculating the position for both points on the X axis. For the first point, when [Points]=1, we want to use our [Line ID] value and subtract 1, so we’re starting at the beginning of our segment (ex. line 1 will start at 0, line 2 will start at 1, line 3 will start at 2, and so on). When [Points]=2, we are going to use just the [Line ID] value (ex. line 1 will end at 1, line 2 will end at 2, line 3 will end at 3). And then we’re just using our [Jitter] field and our “Scale” parameter to jitter these points a little bit, similar to what we did with the “Outer” lines. You may notice that there is a “*2” in these calculations. I added these so I could re-use my same parameters, but could add a little extra jitter to the Cross Lines. I figured if these were actually being done by hand there would be a lot more variation in these lines, compared to the “Outer” lines.

Now let’s calculate our Y coordinates. Similar to how we calculated the Y coordinates for the “Outer” lines, we want one of our points to be half the width of the bar above our starting point, and the other one, half the width of the bar below the starting point. And then we want to jitter them. Here’s the calculation for the Y coordinates.

Cross_Y = if [Points]=1 then [Rank]-([Bar_Width]/2)+([Jitter]*[Scale_Bar_Outer_Height]*2) else [Rank]+([Bar_Width]/2)+([Jitter]*[Scale_Bar_Outer_Height]*2) END

Now this is a little bit confusing because we reversed our axis in an earlier step. So, for Point 1, instead of adding half of the width of the bar to our starting point, the [Rank] field, we need to subtract it from the starting point, to get it to appear above the bar (because the axis is reversed). So when [Points]=1 we’ll subtract half of the width of the bar ([Bar_Width]/2) from the starting point, [Rank]. When [Points]=2, we’ll add half of the width of the bar to the starting point. And then once again we’re using the [Jitter] field, the “Scale” parameter, and then multiplying by 2 to get a little extra jitter. If you wanted to reverse the direction of these lines, so they go from top right to bottom left, just change the calc so when [Points]=1 you add, and when [Points]=2 you subtract.

Now let’s build it.

  • Drag [Line Type] to the filter shelf and filter on “Cross Lines”
  • Right click on [Cross_X], drag it to Columns, and when prompted, choose [Cross_X] without aggregation
  • Right click on [Cross_Y], drag it to Rows, and when prompted, choose [Cross_Y] without aggregation
  • Change the Mark Type to “Line”
  • Right click on [Line ID], select “Convert to Dimension” and then drag [Line ID] to Detail
  • Right click on [Rank], select “Convert to Dimension” and then drag [Rank] to Detail
  • Right click on [Points], drag it to Path, and when prompted, choose [Points] without aggregation
  • Right click on the Y-axis, select “Edit Axis”, and check the box labelled “Reverse” under Scale

Once complete, you should have 50 “Cross Lines” for each of your “bars”.

Now we just need to bring it all together

Combining the Lines

We have our “Outer” lines, and we have our “Cross” lines, and because we have separate data points for each of these (because of the way we structured our data) we can bring them together in the same view pretty easily. We just need to 2 more “Final” calculations for the X and Y coordinates.

Final_X = if [Line Type]=’Outer Lines’ then [Outer_Bar_X] else [Cross_X] END

Final_Y = if [Line Type]=’Outer Lines’ then [Outer_Bar_Y] else [Cross_Y] END

These are pretty straightforward, but basically, if the [Line Type]=”Outer Lines” use the X and Y values from the “Outer_Bar” fields. Otherwise, use the X and Y values from the “Cross” fields. Now let’s build our “bars” with these “Final” calcs.

  • Right click on [Final_X], drag it to Columns, and when prompted, choose [Final_X] without aggregation
  • Right click on [Final_Y], drag it to Rows, and when prompted, choose [Final_Y] without aggregation
  • Change the Mark Type to “Line”
  • Right click on [Line ID], select “Convert to Dimension” and then drag [Line ID] to Detail
  • Right click on [Rank], select “Convert to Dimension” and then drag [Rank] to Detail
  • Drag [Line Type] to Detail
  • Right click on [Points], drag it to Path, and when prompted, choose [Points] without aggregation
  • Right click on the Y-axis, select “Edit Axis”, and check the box labelled “Reverse” under Scale

And now you should have everything together on the same view!

Wait…that doesn’t look right. We don’t want all of those extra “Cross” lines on our shorter bars. Luckily, we can filter those out pretty easily with a calculated field. This is just a boolean calc that checks to see if the Line ID is less than the length of the bar. Remember from earlier that the Line ID corresponds to the right side, or the end of each of these “Cross” lines. So we only want to keep the lines where that value is less than the length of the bar.

Extra Lines Filter = [Line ID]<=[Outer Bar Length]

Now just drag the [Extra Lines Filter] field onto the Filter shelf, and filter on TRUE and voila!

There is one more step that’s completely optional. The way we set up this data source, we can have up to 50 “Cross” lines for the largest bar. But maybe you want less than that. I like to make my visualizations as dynamic as possible so I can play around with how it looks. Earlier we created a parameter called [Cross Lines]. We can use that parameter to determine how many lines we want to use. We’re just going to create one additional calculated field.

Max Cross Lines Filter = [Line ID]<=[Cross Lines]

Just drag that field onto the Filter shelf, filter on TRUE, and then right click on the pill and choose “Add to Context”. Now you can adjust the number of lines, and in doing so, the spacing between the lines. Here’s what it looks like with 30 lines instead of 50.

If you want to use more than 50 lines, just add some additional rows to the “Lines” densification table.

Final Touches

So now our view is built, but there is one critical piece of information missing from our chart…Row Labels. There are a few different ways you can add these, but I’m going to cover two quick options; Shapes and Labels.

For the viz that I shared earlier, I was publishing it to Tableau Public, which has pretty limited options when it comes to fonts, and I really wanted a “hand-drawn” font. What I ended up doing was creating custom shapes for each of my labels in PowerPoint. If you decide to go this route, one thing you want to make sure that you do is to set the size of each of the text boxes equal. If the text boxes are different sizes when you save them as images, it will look like the text is a different size for each value because Tableau will attempt to “normalize” them.

So first, create your shapes in PowerPoint. Here, I inserted 10 text boxes, typed my movie names, set the alignment to “Right”, and then set the Font to “Caveat”. Then I clicked and dragged to highlight all 10 text boxes, and in the top right corner of PowerPoint, in the Shape Format options, I set the “Width” so that they would all be the same size. regardless of how long the text in each box actually is.

Then I right-clicked on each image, saved them to a folder in my “Shapes” repository. Finally, I created a new sheet using the “Shapes” mark type, positioned them by Rank, and then fixed and reversed the axis so they would align with the bars. Then you can throw these two sheets in a container on your final dashboard and have something like this.

So that’s an option if your data is static and you don’t have a lot of values. This would be nearly impossible to maintain if new values were constantly being introduced, and would be way too much work if there were a lot of values in your data source. In those cases, you may need to go with more traditional labels and be limited to the available fonts. But even that can be a little bit tricky because these are lines, not bars.

For this we need one more calculated field. We only want to label 1 point for each of our bars but we can’t filter out any points. We also can’t use a calculation that results in some null values and some populated values for a given Line Type (because it can inadvertently remove sections of the lines we worked so hard to draw).

Label Name = if [Line Type]=’Outer Lines’ then [Name] END

Now just drag the [Label Name] field to Label and then set the Label options as follows.

You can choose whichever font type and size you prefer, but make sure to set the Alignment to “Top Left’, select “Line Ends” under Marks to Label, and under Options, de-select “Label end of line”. Between the calculated field and these options, only 1 Label will appear per bar, and it will appear to the top left of Point 1 of the “Outer” line (which is the bottom left point in each bar). It should end up looking something like this.

Those are a couple of ways to add Row Labels to your “hand-drawn” bar charts. If you want to add value labels as well you can follow a pretty similar process, but it’s a little trickier. This post is already long enough so I’m not going to go into that, but if you make it this far and want to add value labels, please reach out and I’d be happy to help you. Or you can take the easy way out and do what I did, and just create an image of a “hand-drawn” axis and add it to your dashboard.

Thank you so much for reading, and keep an eye on the blog for more ‘Totally Useless Charts & How to Build Them’!

Categories
How-To's Tableau Techniques Totally Useless Charts

Totally Useless Charts & How to Build Them – Lotus Flowers

Welcome to our new series, Totally Useless Charts & How to Build Them. In each installment of this series we’ll look at one very custom chart, something with almost no real use cases, and we’ll walk through, step by step, how to build it. The purpose of this series isn’t necessarily to teach you how to build these specific useless charts, it’s more about talking through the techniques, the approach, and the thought process behind each chart. Our hope is that seeing how we went about building these will help you with your own custom charts. But if you do somehow find a great use case for one of these charts, by all means, please download the workbook and use it as your own.

In this first installment we’re going to learn how to build Lotus Flowers in Tableau. It’s not a requirement, but it may be a good idea to review Part 1 and Part 2 of the Fun With Curves Series before proceeding. To follow along, you can download the workbook here, and the data here.

Lotus Flower

First, let’s take a look at what we’re trying to build. Below is a lotus flower with 10 petals, which means we have a total of 11 polygons; 1 circle and 10 petals. The circle is fairly easy to build using the techniques in Part 1 mentioned above. The petals are a little more complicated. But first thing’s first…we need some data.

Building Your Data Source

Let’s start with our data. For this example we’re going to build 12 lotus flowers and we’re going to use the value from our data source to size the flowers appropriately. We’ll start with the tab titled ‘Source Data’.

Next, we’re going to do some densification to get the number of polygons needed for each of the flowers. Below I have 1 record for the Circle and 24 records for the petals. We’re going to build this in a way that will let you choose how many petals you want to display (up to 24). This data can be found in the ‘Polygons’ tab in the sample data.

Now we’re going to join these two sources together using a join calculation (value of 1 on each side). The result will be 25 records for each of our 12 ‘Base’ records.

Next, we need to do a little more densification, but this time it’s a little trickier. For our circle, we want at least 50 points for a relatively smooth curve. For our petals, we actually need to draw 2 lines for each petal, one for the left side of the petal (Min) and one for the right side of the petal (Max), and then join those together. Pretty confusing right? We’ll talk about this in a lot more detail. This table is a little too large to include a screenshot, but take a look at the ‘Densification’ tab in the sample data.

For our circles, we have 50 records. We have two numerical fields, [Points] and [Order], that both run from 1 to 50 and a [Type] field to identify that these points are for our circles. For our petals, we have 100 records. We still have the same two numerical fields, but the values are a little different. We have an [Order] field that runs from 1 to 100, and a [Points] field that runs from 1 to 50 and then back down from 50 to 1. We also have a [Side] field with values of Min or Max. The Min records will be used to draw the left side of our petals. The Max records will be used to draw the right side of our petals. And then we have a [Type] field to identify that these records are for our petals. Now we just need to join this table to our data source on the [Type] Field.

Building Your Circles

If you have read through Part 1 of the Fun With Curves series, then you may remember that in order to draw a circle in Tableau, we only need 2 inputs; the distance of each point from the center of the circle (the radius), and the position of each point around the circles (represented as a percentage).

Let’s start with the first input, the radius. We are going to size our circles based on the Value field in the Source Data. We want the area of our circles to represent the value in the data. So we have the area of each circle, we just need to use those values to calculate the radius of each circle. We can do this with the simple calculation below.

Radius = SQRT([Value]/PI())

Next, we need to calculate the position of each point around the circle. I’m not going to go into too much detail on this, but you can read more about it in the post mentioned above. To calculate this, we need the maximum number of points for our Circles (50), and we need the [Points] field (values 1 thru 50). For the max point calculation I am going to use an LOD because the max number of points for our circles, may not always align with the max number of points in our data source (but in this case it does).

Max_Point = {FIXED [PolygonType] : MAX([Points])}

Circle_Position = ([Points]-1)/([Max_Point]-1)

Next, we just need to plug the [Radius] and the [Circle_Position] values into our X and Y formulas for plotting points around a circle.

Circle_X = [Radius]* SIN(2*PI() * [Circle_Position])

Circle_Y = [Radius]* COS(2*PI() * [Circle_Position])

Now, let’s draw our circles

  • Right click on [Circle_X] and drag it to columns. When prompted, choose [Circle_X] without any aggregation
  • Right click on [Circle_Y] and drag it to rows. When prompted, choose [Circle_Y] without any aggregation
  • Right click on [Base_ID], change it to a Dimension, and drag it to Detail
  • Right click on [Order], change it to a Dimension, and drag it to Path
  • Drag [Type] to Filter Shelf and filter to ‘Circle’
  • Change the Mark Type to Polygon

Now you should have something that looks like this.

Although it looks like one big circle, we actually have all 12 circles in this view. They’re just stacked on top of each other. So next we need to space these out a little bit. There are a lot of different techniques to do this, but here’s one I like to use to create Trellis Charts. This technique works great when you have a sequential ID field, which we do (Base_ID).

First, we’re going to create a numeric parameter that will allow us to choose the number of columns we want to create. We’ll call the parameter [Column Count] and set the value to 3. Next, we’re goin to use the [Base_ID] field to break our circles into columns and rows, starting with row.

Row = CEILING([Base ID]/[Column Count])

Column = [Base ID]-(([Row]-1)*[Column Count])

Now right click on both of these fields, change them to Dimensions, and then drag them to the appropriate shelf (Row to Rows, Column to Columns). The result should look something like this.

Building Your Petals

Alright, so this part is a little more complicated. I’m going to start by reviewing the basics of how you build these shapes, but I’m going to skim over the calculations since those will change significantly once we try to build these petals around our circle. No need to follow along with the workbook during this section.

So here are the basics. Let’s start by drawing a Bezier Curve with 4 control points. Our line is going to start at 0,0 and end at 5,10. Wow, this is easy, we already have the coordinates for 2 of the points!

Let’s take a look at our inputs. Our line will have a height of 10 and a width of 5. I’ve also built 2 parameters that we’ll use to calculate the 2nd and 3rd set of points. You can experiment with different values here, but these seem to work pretty well. We need a total of 8 values (4 sets of X and Y).

  • Point 1 will be the start of the line. In this case, it’s 0,0
  • Point 2 will appear on the same X axis as Point 1, but will be somewhere between the start and end of the line on the Y axis. I like to place it two thirds of the way, or .67 (the value in the P2 Parameter Input above). So the coordinates for Point 2 will be 0 and 6.7 (P2 Parameter x Height of the line)
  • Point 3 will appear on the same X axis as Point 4, and will appear somewhere between the start and end of the line on the Y axis (similar to P2). I like to place it halfway, or .5 (the value in the P3 Parameter Input above). So the coordinates for Point 3 will be 5 and 5 (P3 Parameter x Height of the line).
  • Point 4 will be the end of the line. In this case, it’s 5,10

If you were to plot these 4 points, you would have a jagged line like you see in the image above. But look what happens when we plug those values into our Bezier calculations

X = (1-[T])^3*[P1_X] + 3*(1-[T])^2*[T]*[P2_X] + 3*(1-[T])*[T]^2*[P3_X] + [T]^3*[P4_X]

Y = (1-[T])^3*[P1_Y] + 3*(1-[T])^2*[T]*[P2_Y] + 3*(1-[T])*[T]^2*[P3_Y] + [T]^3*[P4_Y]

Alright, we are halfway there! Kind of. So now we have a line that will create 1/2 of one of our petals. But in order to turn this into a petal shaped polygon, we need another line that’s a mirror image of this one.

This is where the Min and Max records come in. We need to calculate our 4 sets of coordinates for both sides. Luckily, most of the values are actually the same. P3 and P4 are going to be identical for both lines. And the Y values for P1 and P2 are the same. The only differences are the X values for P1 and P2. And to calculate those we just add the width of the whole petal (width x2) to our starting point. And if we were to plug these coordinates into the same calculations, we have this.

Now this is where the [Order] field comes into play. To make this one single polygon instead of two separate lines, we can use the [Order] field on Path and change the Mark Type to polygon

On the Left (Min) side, we have points 1 thru 50, running from the bottom left up to the top middle. On the right (Max) side, we have points 1 thru 50 running from the bottom right up to the top middle. But then we have the [Order] field (on label in the image above). This field runs from the bottom left to the top middle to the bottom right, in one continuous flow, from value 1 to 100. This is what makes it a single continuous polygon.

Ok, so that’s how we would build 1 single petal shaped polygon, perfectly positioned facing directly upward. But that’s not what we’re trying to do. We’re trying to build a dynamic number of petals, evenly spread around a circle and facing outward in the appropriate directions. So let’s do that.

Building Your Petals (for real this time)

We’re going to use a similar approach to what was described above, but everything needs to be plotted around a circle. So any calculations we use to determine our 4 points are going to have to run through those X and Y calculations for plotting points around a circle. That means, for all of our points, P1 thru P4 for both sides, we need to calculate two things; the distance from the center of the circle, and the position around the circle. But before we calculate those specific points there are a few other calculations that we’ll need. We also need a parameter, called [Petal Count] that will allow us to select how many petals we want. This should be a numeric parameter, and let’s set the value to 10 (I recommend using a range, allowing values from 4 to 24)

T = ([Points]-1)/([Max_Point]-1) – this is the same as the [Position] calc used earlier. It’s used to evenly space points between 0% and 100%

Petal_Count_Filter = [Polygon ID]<=[Petal Count] – this will be used as a filter to limit the number of petals displayed to what is selected in the [Petal Count ] parameter

Petal_Width = 1/[Petal Count] – this calculates the total position around the circle that will be occupied by each petal. For example, if there were 10 petals, each one would occupy 1/10 of the space around the circle, or .10

Petal_Side_Position = IF [Side]=’MIN’ THEN ([Polygon ID]-1)*[Petal_Width] ELSE [Polygon ID]*[Petal_Width]
END – this calculates the position of the start of each Min line and Max line. If there were 10 petals, the Min side of the 2nd petal would be at position .1 or (2-1)*.1, and the Max side of the petal would be at position .2, or 2*.1. The Min value will share the same position as the Max value of the previous petal. The max value will share the same position as the Min value of the next petal

Petal_Middle_Position = ([Polygon ID]/[Petal Count]) – ([Petal_Width]/2) – this calculates the position of the center of each petal. If there were 10 petals, the center of petal 3 would be at .25, or (3/10) – (.1/2). This is also halfway between the position of the Min line and the Max line.

Alright, now we can calculate all of our coordinates. Let’s start with P1. For the first input, we want this point to start right at the edge of our circle. So the distance from the center is going to be equal to the radius of the inner circle. So the first input is just [Radius]. For the second input, we’ll use the the [Petal_Side_Position] we calculated above.

P1_X = [Radius]* SIN(2*PI() * [Petal_Side_Position])

P1_Y = [Radius]* COS(2*PI() * [Petal_Side_Position])

If we were to plot these points for 12 petals, we would end up with 24 points, but it would appear that we only 12 because each is overlapping with another point. But this gives us the outside edges of each of our petals

Now onto P2. This one is a little more complicated. We’re going to use P1 as a starting point for this calculation, instead of the center of the inner circle. Now we need to calculate the distance from P1 where we want our next point to appear. First, we need to determine the length of the entire petal. I like to use a parameter for this so I can dynamically adjust the look of the flowers. So let’s create a parameter called [Petal_Length_Ratio]. This is going to be a number relative to the radius, so a ratio of 1 would set the length of the petal equal to the radius of the circle. A value of .8 would set the length of the petal equal to 80% of the radius, and so on. I usually go with a value somewhere between .5 and 1. We’ll use this along with the radius, so that the petals of each flower are sized appropriately based on the size of their inner circle. Next, we need to position this point somewhere between the start of the line and the end of the line. As I mentioned earlier, I like to place it two thirds of the way (P2_Parameter from the previous section). So the first input, the distance from P1, is going to be the radius x the length ratio x the P2 parameter. For the second input, we’re going to use the [Petal_Middle_Position] because we want this side of the line to follow the same path as the line with P3 and P4. If we were to use the [Petal_Side_Position] field, we would end up with really wide, strange looking petals. This will probably make more sense a little further along. For now, let’s plug those values into our X and Y calcs.

P2_X = [P1_X] + (([Radius] * [Petal_Length_Ratio] * [P2_Parameter]))* SIN(2*PI() * [Petal_Middle_Position])

P2_Y = [P1_Y] + (([Radius] * [Petal_Length_Ratio] * [P2_Parameter]))* COS(2*PI() * [Petal_Middle_Position])

P3 is a little more straight forward. For the first input, we’re going to calculate the distance from the center of the inner circle. And then we’ll use a similar approach to what we did for P2. The first input will be the radius + (the radius x the length ratio x the P3 parameter). As I mentioned in the earlier section, I like to set this parameter to .5. And once again, we’re going to use the [Petal_Middle_Position] field for the second input.

P3_X = ([Radius]+([Radius] *[Petal_Length_Ratio] * [P3_Parameter]))* SIN(2*PI() * [Petal_Middle_Position])

P3_Y = ([Radius]+([Radius] *[Petal_Length_Ratio] * [P3_Parameter]))* COS(2*PI() * [Petal_Middle_Position])

P4 is almost identical to P3, except we don’t need the length ratio. We want this point to appear at the end of the line. So we can just remove that from the calc.

P4_X = ([Radius]+([Radius] * [Petal_Length_Ratio])) SIN(2*PI() * [Petal_Middle_Position])

P4_Y = ([Radius]+([Radius] * [Petal_Length_Ratio])) COS(2*PI() * [Petal_Middle_Position])

We’re almost there! If we were to plot these points for the first petal in our lotus flower, it would look like this. It looks very similar to what we reviewed in the previous section, but with one very important difference…everything is at an angle…which is what we wanted.

All that’s left to do is to plug all of these points in our Bezier calcs and then build our polygons!

Petal_X = (1-[T])^3*[P1_X] + 3*(1-[T])^2*[T]*[P2_X] + 3*(1-[T])*[T]^2*[P3_X] + [T]^3*[P4_X]

Petal_Y = (1-[T])^3*[P1_Y] + 3*(1-[T])^2*[T]*[P2_Y] + 3*(1-[T])*[T]^2*[P3_Y] + [T]^3*[P4_Y]

Now the polygons. Let’s build this as a Trellis chart, just like we did with the Circles. So drag [Row] on to Rows and [Column] onto Columns. And then;

  • Right click on [Petal_X] and drag to Columns. When prompted, select [Petal_X] without aggregation
  • Right click on [Petal_Y] and drag to Rows. When prompted, select [Petal_Y] without aggregation
  • Drag [Type] to Filter Shelf and filter to ‘Petal’
  • Drag [Petal_Count_Filter] to Filter Shelf and filter to TRUE. Right click and ‘Add to Context’
  • Drag [Polygon_ID] to Detail
  • Drag [Order] to Path
  • Change Mark Type to Polygon

We’re so close! Your sheet should look like this

The only thing left to do is to combine the Circle polygons with the Petal Polygons. We have separate data for them, all we need to do is get them on the same sheet. So we’ll create two more simple calcs to bring it all together.

Final_X = IF [Type]=’Circle’ THEN [Circle_X] ELSE [Petal_X] END

Final_Y = IF [Type]=’Circle’ THEN [Circle_Y] ELSE [Petal_Y] END

Now just replace [Petal_X] and [Petal_Y] with [Final_X] and [Final_Y] and drag [Type] from the filter shelf on to Color and you should have your lotus flowers!

The Final Touches

The hard part is done, now to make it look pretty. Play around with some of the parameters until you get the look that you like. Adjust the [Petal Count], the [Column_Count], the [Petal_Length_Ratio], and even the [P2_Parameter] and [P3_Parameter] if you wanna get crazy.

Next, throw some color on there. You could make the color meaningful to encode some data, or you could do what I just did and color it randomly. I used the calc below and then just assigned one of the color palettes I have saved.

Color = [Type] + STR([Base ID])

And that’s it! If you made it this far, please reach out and let me know what you thought, and what you came up with. Thank you so much for reading, and keep an eye on the blog for more ‘Totally Useless Charts & How to Build Them’